导语

最近因为上海的疫情，被关在家里，有点闷坏了，小区里的快递或者外卖，也不允许下楼取，由小区保安统一配送，保安还需要定时去巡查，看看小区有没有违规下楼，小区有没有人在随意走动，我们小区有8栋楼，虽然不大，但楼宇间有绿化带阻隔，加上小区保安人手有限，怎样合理规划路径（保证所有路径都经过，又不重复走），倒是一个有趣的图论问题。我突然想到了哥尼斯堡七桥经典问题，相传18世纪初普鲁士的哥尼斯堡，有一条河穿过，河上有两个小岛，有七座桥把两个岛与河岸联系起来（如下图）。有个人提出一个问题：一个步行者怎样才能不重复、不遗漏地一次走完七座桥，最后回到出发点。

自己画的图有点丑，但应该比较好理解，A、D是两个小岛，B、C是两边的陆地。

哥尼斯堡的七座桥

1736年29岁的欧拉向圣彼得堡科学院递交了《哥尼斯堡的七座桥》的论文，在解答问题的同时，开创了数学的一个新的分支——图论与几何拓扑，也由此展开了数学史上的新历程。欧拉的名声如雷贯耳，往往成功的大师，都是有心人，对生活中遇到的问题，愿意进行深入的分析和思考。在论文中，欧拉对哥尼斯堡的七座桥问题进行了抽象与转换，他认为岛和两边的河岸都是点，桥就是连接点的边，那么能否不重复地走过所有的桥，又不重复，就转换为能否一笔画出对应的图（点和边组成的图），并且没有重复的笔画。

首先，我们来了解下关键的一个概念：度数，即每个点连接的边数量。那么可以把点分为：

• 奇点：点的度数为奇数的点，即连接此点的边数量为奇数；
• 偶点：点的度数为偶数的点，即连接此点的边数量为偶数；

我们使用一笔画出一个图来，如下图所示，红色的点就是偶点，蓝色的点就是奇点，落笔的点就是奇点之一，另外一个奇点就是收笔的点。中间的所有点都是偶点，一进一出，必然度数是2、4、6、8等情况。而奇点有2个，分别是落笔的点和收笔的点，不可能出现第三个奇点。

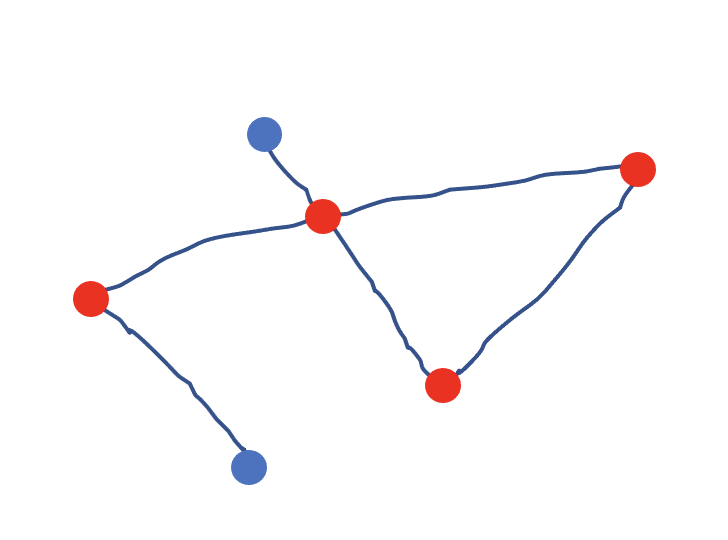
如果把落笔点和收笔点连接起来，理解为两个奇点连接起来，那么图中所有的点都是偶点。如下图所示：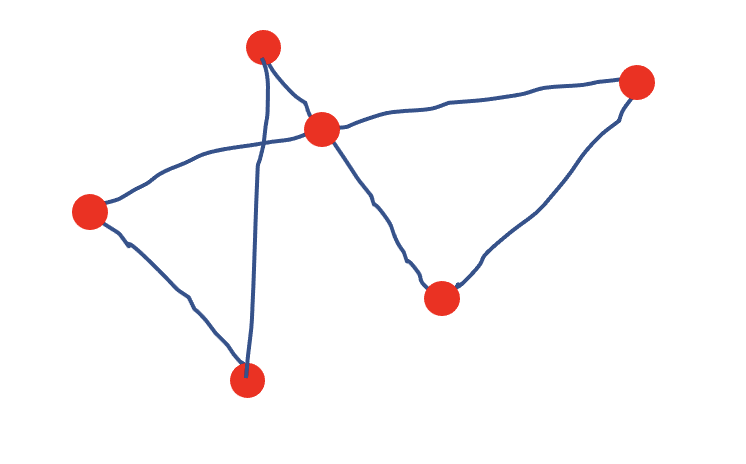

在1736年，大数学家欧拉提出了一个图如果一笔不重复地画出来，需要的充要条件是，该图只有0个或者2个奇点，如果存在0个奇点，图中存在欧拉回路，如果存在2个奇点，图中存在欧拉路径。回到哥尼斯堡七桥问题，抽象出来的图如下：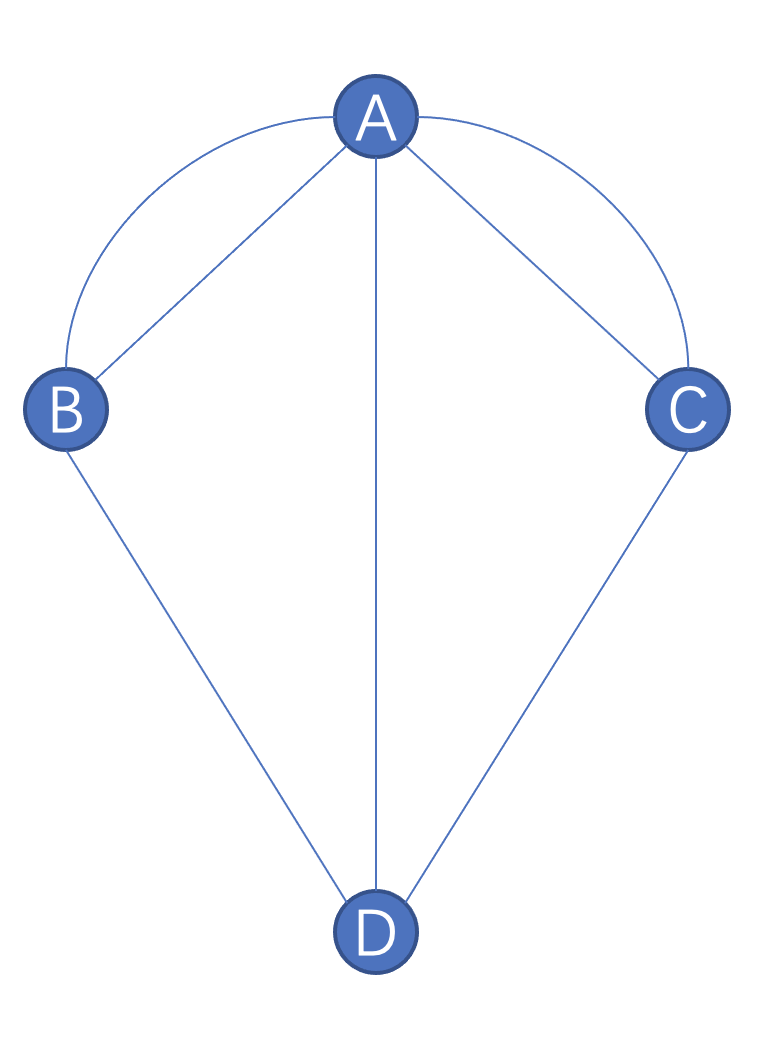

可以看到4个点都是奇点，所以欧拉说，不可能做到不重复、不遗漏地一次走完七座桥。既然这个图不能一笔画出来，那么究竟几笔能画出来，欧拉也给了答案。图的奇点总是成对出现的，因为有一个落笔点，必然会有一个收笔点，如果一张图有2k(k >= 1)个奇点，那么欧拉认为有以下3个推论：

• 此图可以通过k笔画出
• 添加k-1条边，保证存在欧拉路径
• 添加k条边，保证存在欧拉回路

回到我们小区送东西的场景，简化为下图：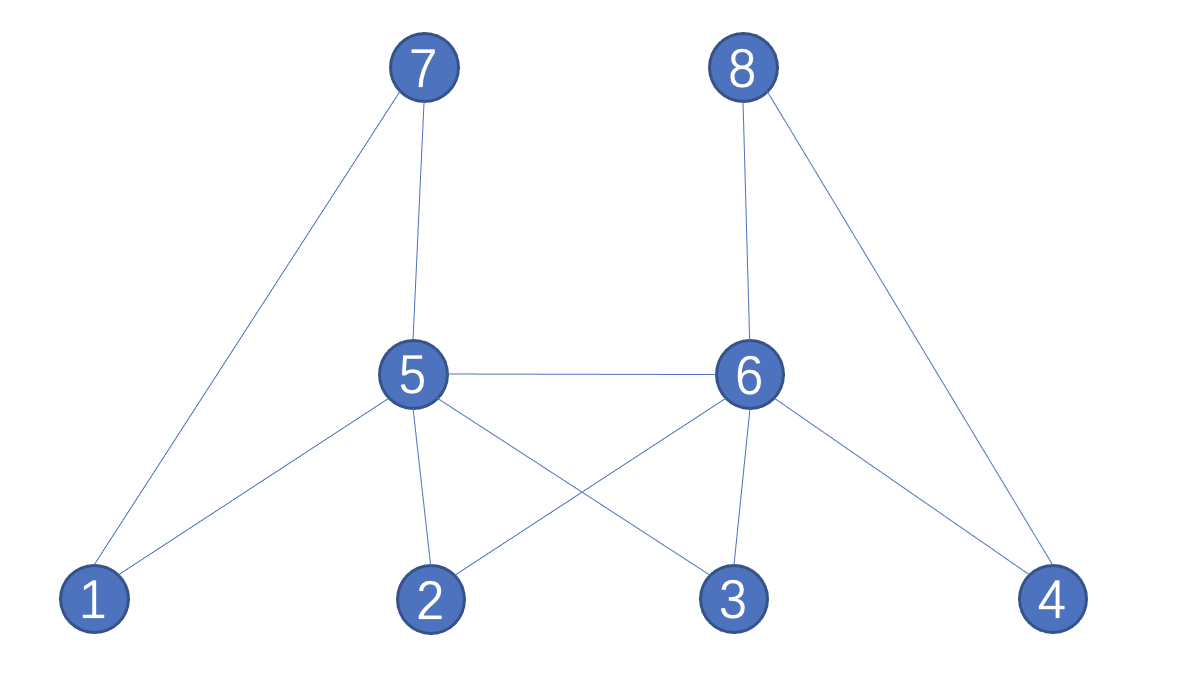

一共8栋楼，如果小区保安走一遍，保证每条路径都要走到，又不能重复，存在这样的路径，比如：

很幸运，我们小区还是有这样一条路径，可以保证保安巡查时不走重复路的，但又走遍了所有的角落。有些实际生活中的场景，也适合使用欧拉回路来规划，比如在旅游景区的线路规划（游客都不希望走回头路，但又希望每一条路都走一遍），也比较适合。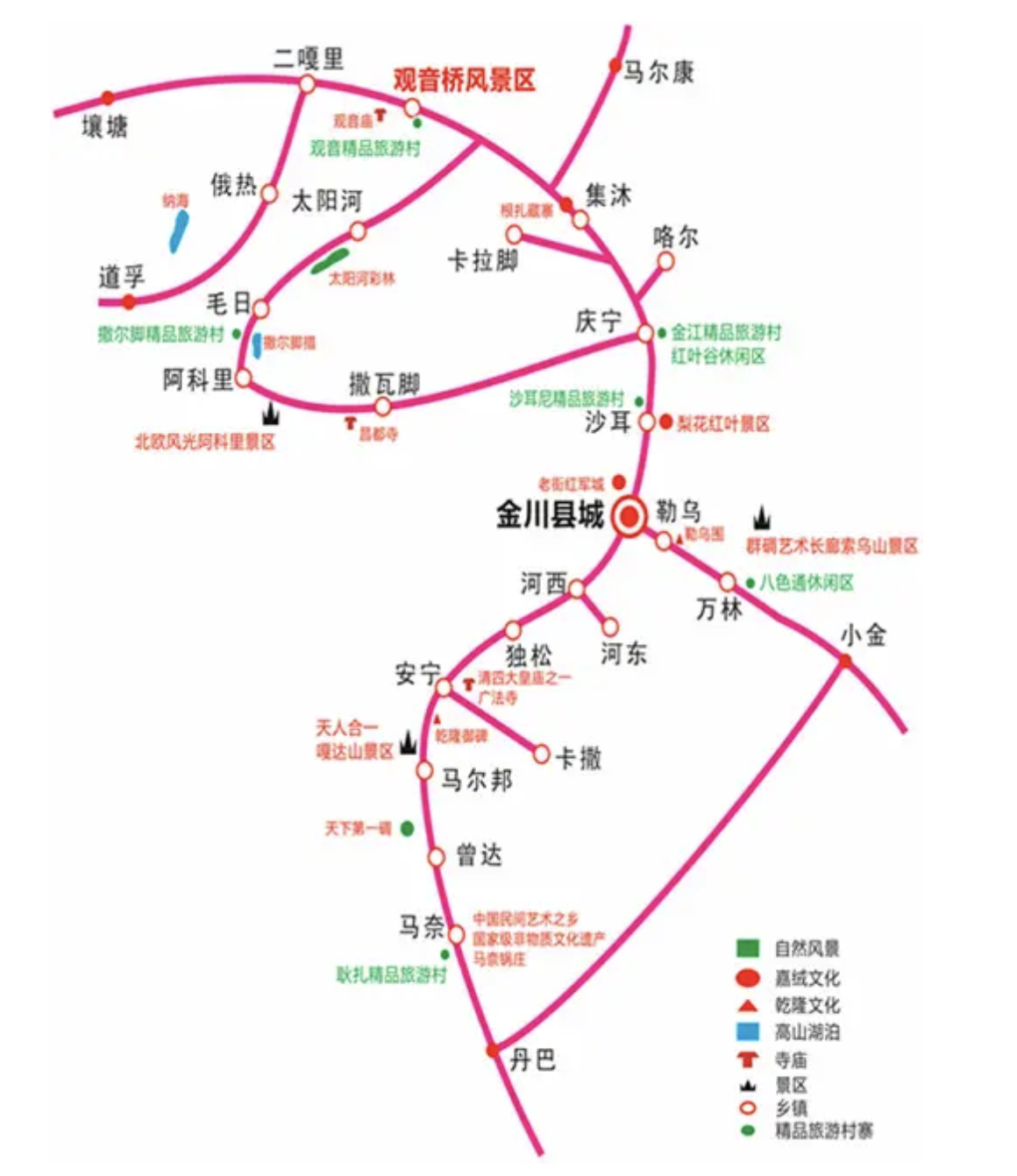

如上图，怎么添加线路，使得可以保证旅游景区存在欧拉回路，是不是特别有意思和实用？

结束语

图论中有很多有趣的问题，显然300多年前，欧拉打开了一扇图论的大门，还有一些问题，比如需要走遍图中所有点一次（但不能重复经过点），边不需要都走，有没有合适的判定方法或者算法，显然欧拉回路或者路径是不适用的，这个也有相应的图论算法，叫哈密尔顿回路/路径，单独写文章介绍，在此不详述了。