前言

个人认为，这是一道非常经典的 LeetCode Hard 题目，第一次碰到时，感觉觉得如此之精妙，想破脑袋也不会想到使用什么样合适的数据结构去解决这道问题。时隔快5年，在2024年农历新年最后一个工作日，重温下这道经典的题目。

题目描述

中位数是有序序列最中间的那个数。如果序列的长度是偶数，则没有最中间的数；此时中位数是最中间的两个数的平均数。

例如：

[2,3,4]，中位数是 3
[2,3]，中位数是 (2 + 3) / 2 = 2.5
给你一个数组 nums，有一个长度为 k 的窗口从最左端滑动到最右端。窗口中有 k 个数，每次窗口向右移动 1 位。你的任务是找出每次窗口移动后得到的新窗口中元素的中位数，并输出由它们组成的数组。

示例：

给出 nums = [1,3,-1,-3,5,3,6,7]，以及 k = 3。

窗口位置 中位数
--------------- -----
[1 3 -1] -3 5 3 6 7 1
1 [3 -1 -3] 5 3 6 7 -1
1 3 [-1 -3 5] 3 6 7 -1
1 3 -1 [-3 5 3] 6 7 3
1 3 -1 -3 [5 3 6] 7 5
1 3 -1 -3 5 [3 6 7] 6
因此，返回该滑动窗口的中位数数组 [1,-1,-1,3,5,6]。

提示：

你可以假设 k 始终有效，即：k 始终小于等于输入的非空数组的元素个数。
与真实值误差在 10 ^ -5 以内的答案将被视作正确答案。

原题快速门

说句题外话，以现在卷的程度，是不是很多校招生必会解此题呢，想当年，这样的题目，是不太可能出现在现场笔试题目中的。^.^

解题思路

首先，拿到一道题目后，要分析输入规模，那其实老的题目这点是不太规范的，往往没有给你输入规模的描述，也就少了一些提示。我理解这道题目的输入规模应该如下：
n = len(nums)
1 <= k <= n <= 10^5
那么如果是这样的数据规模，所有O(n^2)的算法可以直接劝退，不用费脑子和精力去想了。接下来，要仔细想下题目的考点是哪一个，或者哪几个组合。显然这道题目非常贴心的告诉你一个考点，滑动窗口，什么是滑动窗口，题目的示例解释的非常清楚了，k表示滑动窗口的长度，窗口往右滑动时，前面的数出窗口，后面的数进入窗口，就是这么个过程。其次，要求窗口内数据的中位数，如果每次暴力的重新计算，那么需要排序，取中间值，显然这个方案的复杂度，最坏情况下会变成O(n^2logn)，应该是过不了testcase，那么这里就要引入数据结构，以O(1)时间计算中位数，如果滑动窗口内的数字保存在一个有序数组，那么计算中位数的复杂度为O(1)就很轻松了，但是删除和添加一个元素到有序数组，操作是O(N)的，那什么数据结构删除和添加一个元素是O(logn)以下的复杂度呢？啊，想到了，类似堆或者红黑树的数据结构。
那怎样使用有序的这些数据结构，实现滑动窗口中位数呢？最巧妙的设计在于，使用两个堆或者有序树的实例，一个维护前半段，一个维护后半段，那么中位数和前半段的最大值和后半段的最小值相关。如果是堆的话，前面半段使用最大堆，后面半段使用最小堆。如下图所示：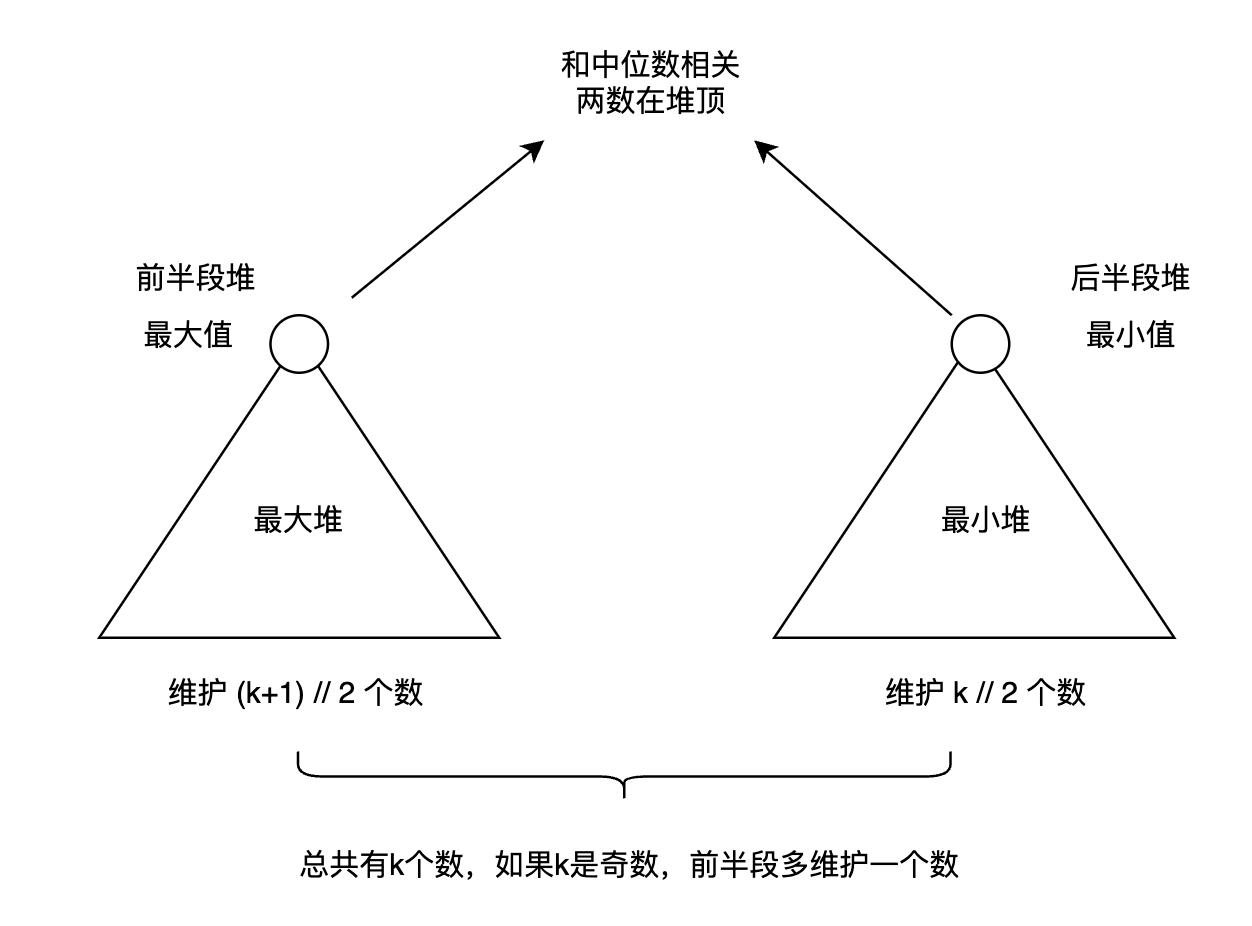

这里还有一个细节点，如果k是偶数，那么前半段和后半段的数字数量相等，否则前半段多维护一个数，所以前半段维护数字的数量是 k+1 除以 2 下取整，后半段维护数字的数量是 k 除以 2 下取整。所以当 k 为奇数时，前半段堆最大值就是中位数，否则，需要将两个堆顶的数字取平均。

代码实现

通过上面的分析，思路有了，我实际实现时，使用了Python3，以及SortedList这个有序List（底层实现采用了二分查找和分块算法。在插入元素时，它会将列表分块，并在每个块内部使用二分查找来维护有序性。这样可以在保证列表有序的同时，提高插入和查找元素的效率），效果和堆是类似的，就是优化插入和删除元素的时间复杂度。代码如下：

from sortedcontainers import SortedList

class Solution:
def medianSlidingWindow(self, nums: List[int], k: int) -> List[float]:
    n = len(nums)
    l = (k+1) // 2
    r = k // 2

    L = SortedList(nums[:k])
    R = SortedList()

    def L2R():
        x = L.pop()
        R.add(x)

    def R2L():
        x = R.pop(0)
        L.add(x)

    while len(L) > l:
        L2R()

    ans = []
    if l > r:
        ans.append(L[-1])
    else:
        ans.append((L[-1] + R[0]) / 2)

    for i in range(k, n):
        out_val = nums[i-k]
        if out_val in L:
            L.remove(out_val)
        else:
            R.remove(out_val)
        
        in_val = nums[i]
        if not L or in_val < L[-1]:
            L.add(in_val)
        else:
            R.add(in_val)
        
        if len(L) == l-1:
            R2L()
        elif len(L) == l+1:
            L2R()

        if l > r:
            ans.append(L[-1])
        else:
            ans.append((L[-1] + R[0]) / 2)
    
    return ans

结论

上述实现的代码，时间复杂度O(nlogk)，空间复杂度O(k)。所谓温故知新，最近也有些堆顶堆的题目出现在周赛上面，只是比起以前的题目，现在的题目不会直接把题目考点赤裸裸写在标题里面，需要你自己抽象转换，这步其实非常难，需要你特别熟悉这些题目考点，才能在关键时刻想到如何转换。