1000^999,999^1000谁大?
导语
记得高中时,老师曾经出过一道题目,1000的999次方和999的1000次方谁大,凭直觉,很多人都说当然是999的1000次方更大,至于为什么,当时很少有同学知道,很多人都这样想的,底数相差1,次方大1的数更大。当年,老师带着大家做了深入的思考和分析,总结出来了规律和原因,结果证明直觉并不可靠。直至最近,我看到一个三进制计算机性能更好的视频,突然把这两个知识串联起来了,再此做一个分享
抽象&分析
当年老师首先要求我们进行题目抽象,1000^999,其实就是有999个1000相乘,这些数的和等于1000*999=999000,而999^1000,就是1000个999相乘,这些数的和也正好是999000,于是,题目就变成了把一个正整数拆成n个正整数的和,是它们的积最大?
那么如何解决抽象出来的问题呢,999000数字太大,不好拆解,那么就使用个小点的数字,比如12,12能怎么拆呢,无非下面几种情况:
12=1+1+1……+1,一共12个1相加,积为1
12=2+2+2……+2,一共6个2相加,积为64
12=3+3+3+3,一共4个3相加,积为81
12=4+4+4,一共3个4相加,积为64
12=5+5+2,积为552,积为50
……
还有其他拆解方法,但是显然,最大的就是拆解为4个3,这时我们就发现了,之前直觉并不对,为什么?因为2^6和3^4相比,次方数2^6比3^4大2,底数小1,但是最后的结果是3^4更大。不管你后面怎么拆,3^4的值最大。仔细看看拆分的方案,规律可以总结为:
- 拆一个正整数为n个正整数相乘,尽可能地多拆3出来,不能拆3,就拆2或者4,坚决不能拆1;
- 如果拆出来的数比3大的越多,乘积就越小,比如上面的4^3和5%2等比3大的拆分方案;
知道了这个规律后,就非常容易判断1000^999和999^1000哪个数更大,显然,999比1000更接近3,999^1000更大。那么上面的规律如何证明呢,我记得老师噼里啪啦写了推导,证明过程如下:
N = x + x + …… + x,把大N拆成n个x的和,n=N/x,要使得f(x) = x^n=x^(N/x)最大。
如果要求f(x)最大,lnf(x)也满足最大,两边取对数lnf(x) = lnx^(N/x),即lnf(x) = (N/x)*lnx。
求导数[lnf(x)]' = N * (1-lnx) / x^2,显然当x > e,导数小于0,是减函数,x < e,导数大于0,是增函数,所以x = e时,lnf(x)最大,e = 2.71818,显然最接近e的正整数就是3,所以规律得证。
联想
最近又看到一个视频,讲得是三进制计算机性能最好,我突然联想到这个曾经学过的知识,后来仔细想了下,视频想表达的观点,应该是三进制比二进制或者十进制表达能力更强,相同的内存大小,如果是三进制,可以表达的数最多。小时候都玩过一个游戏,一组珠串,假设给你100颗珠子,怎样分配,可以使得表示的数字数量最多,结果就是下图: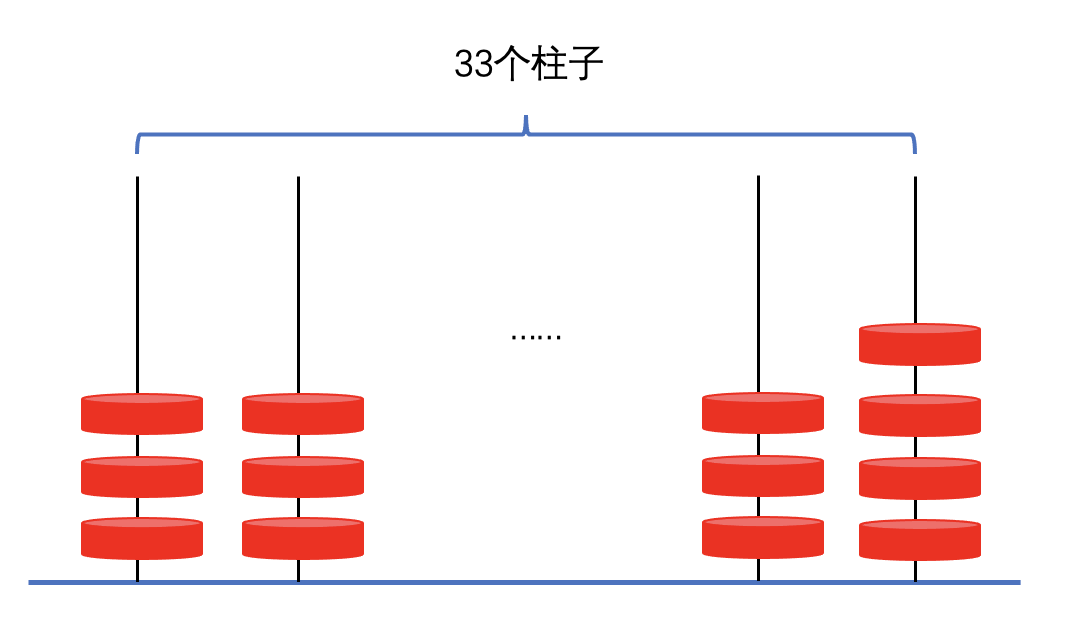
每个柱子上留三颗珠子,可表示3^324个数(计算机里面就是3^324个状态),表达的数量最多。没想到,三进制表达能力最强,在我高中时,老师就把原因告诉了我,哈哈。所以学好数学,培养好逻辑思考能力,真的是终身受用,加油吧,少年。
1
555