Redis Scan命令背后有趣的原理
导语
Redis Scan 命令在实际生产环境中,业务上的在线场景,应该用的不多,但是在某些离线场景,还是有用武之地的,比如对大key的删除(SET、HASH),可以使用Scan进行迭代处理。
KEYS 与 SCAN
由于 Redis 是单线程在处理用户的命令,而 Keys 命令会一次性遍历所有 Key,于是在 命令执行过程中,无法执行其他命令。这就导致如果 Redis 中的 key 比较多,那么 Keys 命令执行时间就会比较长,从而阻塞 Redis。
所以很多教程都推荐使用 Scan 命令来代替 Keys,因为 Scan 可以限制每次遍历的 key 数量。
Keys 的缺点:
没有limit,我们只能一次性获取所有符合条件的key,如果结果有上百万条,那么等待你的就是“无穷无尽”的字符串输出。
keys命令是遍历算法,时间复杂度是O(N)。如我们刚才所说,这个命令非常容易导致Redis服务卡顿。因此,我们要尽量避免在生产环境使用该命令。
相比于keys命令,Scan命令有两个比较明显的优势:
1)Scan命令的时间复杂度虽然也是O(N),但它是分次进行的,不会阻塞线程。
2)Scan命令提供了 count 参数,可以控制每次遍历的集合数。
SCAN的命令语法:
SCAN cursor [MATCH pattern] [COUNT count]
cursor - 游标。
pattern - 匹配的模式。
count - 指定每次遍历多少个集合。
可以简单理解为每次遍历多少个元素
根据测试,推荐 Count大小为 1W。
Scan 返回值为数组,会返回一个游标+一系列的 Key。
大致用法如下:
SCAN命令是基于游标的,每次调用后,都会返回一个游标,用于下一次迭代。当游标返回0时,表示迭代结束。
第一次 Scan 时指定游标为 0,表示开启新的一轮迭代,然后 Scan 命令返回一个新的游标,作为第二次 Scan 时的游标值继续迭代,一直到 Scan 返回游标为0,表示本轮迭代结束。
通过这个就可以看出,Scan 完成一次迭代,需要和 Redis 进行多次交互。
按官方命令手册说明,Scan 命令有如下缺陷:
- 同一个元素可能会被返回多次。 处理重复元素的工作交由应用程序负责, 比如说, 可以考虑将迭代返回的元素仅仅用于可以安全地重复执行多次的操作上;
- 如果一个元素是在迭代过程中被添加到数据集的, 又或者是在迭代过程中从数据集中被删除的, 那么这个元素可能会被返回, 也可能不会, 这是未定义的(undefined);
另外,注意Scan命令的性能和参数Count有关:
原文链接:https://docs.keydb.dev/blog/2020/08/10/blog-post/
Scan背后的原理
先贴下源码:
unsigned long dictScan(dict *d,
unsigned long v,
dictScanFunction *fn,
void *privdata)
{
dictht *t0, *t1;
const dictEntry *de;
unsigned long m0, m1;
if (dictSize(d) == 0) return 0;
if (!dictIsRehashing(d)) {//没有在做rehash,所以只有第一个表有数据的
t0 = &(d->ht[0]);
m0 = t0->sizemask;
//槽位大小-1,因为大小总是2^N,所以sizemask的二进制总是后面都为1,
//比如16个slot的字典,sizemask为00001111
/* Emit entries at cursor */
de = t0->table[v & m0];//找到当前这个槽位,然后处理数据
while (de) {
fn(privdata, de);//将这个slot的链表数据全部入队,准备返回给客户端。
de = de->next;
}
} else {
t0 = &d->ht[0];
t1 = &d->ht[1];
/* Make sure t0 is the smaller and t1 is the bigger table */
if (t0->size > t1->size) {//将地位设置为
t0 = &d->ht[1];
t1 = &d->ht[0];
}
m0 = t0->sizemask;
m1 = t1->sizemask;
/* Emit entries at cursor */
de = t0->table[v & m0];//处理小一点的表。
while (de) {
fn(privdata, de);
de = de->next;
}
/* Iterate over indices in larger table that are the expansion
* of the index pointed to by the cursor in the smaller table */
do {//扫描大点的表里面的槽位,注意这里是个循环,会将小表没有覆盖的slot全部扫描一次的
/* Emit entries at cursor */
de = t1->table[v & m1];
while (de) {
fn(privdata, de);
de = de->next;
}
/* Increment bits not covered by the smaller mask */
//下面的意思是,还需要扩展小点的表,将其后缀固定,然后看高位可以怎么扩充。
//其实就是想扫描一下小表里面的元素可能会扩充到哪些地方,需要将那些地方处理一遍。
//后面的(v & m0)是保留v在小表里面的后缀。
//((v | m0) + 1) & ~m0) 是想给v的扩展部分的二进制位不断地加1,来造成高位不断增加的效果。
v = (((v | m0) + 1) & ~m0) | (v & m0);
/* Continue while bits covered by mask difference is non-zero */
} while (v & (m0 ^ m1));//终止条件是 v的高位区别位没有1了,其实就是说到头了。
}
/* Set unmasked bits so incrementing the reversed cursor
* operates on the masked bits of the smaller table */
v |= ~m0;
//按位取反,其实相当于v |= m0-1 , ~m0也就是11110000,
//这里相当于将v的不相干的高位全部置为1,待会再进行翻转二进制位,然后加1,然后再转回来
/* Increment the reverse cursor */
v = rev(v);
v++;
v = rev(v);
//下面将v的每一位倒过来再加1,再倒回去,这是什么意思呢,
//其实就是要将有效二进制位里面的高位第一个0位设置置为1,因为现在是0嘛
return v;
}
Redis使用了Hash表作为底层实现,原因不外乎高效且实现简单。类似于HashMap那样数组+链表的结构。其中第一维的数组大小为2n(n>=0)。每次扩容数组长度扩大一倍。
Scan命令就是对这个一维数组进行遍历。每次返回的游标值也都是这个数组的索引。Count 参数表示遍历多少个数组的元素,将这些元素下挂接的符合条件的结果都返回。因为每个元素下挂接的链表大小不同,所以每次返回的结果数量也就不同。
关于 Scan 命令的遍历顺序,我们可以用一个小栗子来具体看一下:
127.0.0.1:6379> keys *
1) "key2"
2) "key3"
3) "key1"
4) "key4"
127.0.0.1:6379> scan 0 MATCH * COUNT 1
1) "2"
2) 1) "key2"
127.0.0.1:6379> scan 2 MATCH * COUNT 1
1) "3"
2) 1) "key3"
2) "key1"
127.0.0.1:6379> scan 3 MATCH * COUNT 1
1) "0"
2) 1) "key4"
如上所示,SCAN命令的遍历顺序是:0->2->1->3
这个顺序看起来有些奇怪,我们把它转换成二进制:00->10->01->11
可以看到每次这个序列是高位加1的。
普通二进制的加法,是从右往左相加、进位。而这个序列是从左往右相加、进位的。
相关源码:
v = rev(v);v++;v = rev(v);
Redis Scan 命令最终使用的是 reverse binary iteration 算法,大概可以翻译为 逆二进制迭代,具体算法细节可以看一下这个Github 相关讨论
这个算法简单来说就是:
依次从高位(有效位)开始,不断尝试将当前高位设置为1,然后变动更高位为不同组合,以此来扫描整个字典数组。
其最大的优势在于,从高位扫描的时候,如果槽位是2^N个,扫描的临近的2个元素都是与2^(N-1)相关的就是说同模的,比如槽位8时,0%4 == 4%4, 1%4 == 5%4 , 因此想到其实hash的时候,跟模是很相关的。
比如当整个字典大小只有4的时候,一个元素计算出的整数为5, 那么计算他的hash值需要模4,也就是hash(n) == 5%4 == 1 , 元素存放在第1个槽位中。当字典扩容的时候,字典大小变为8, 此时计算hash的时候为5%8 == 5 , 该元素从1号slot迁移到了5号,1和5是对应的,我们称之为同模或者对应。
同模的槽位的元素最容易出现合并或者拆分了。因此在迭代的时候只要及时的扫描这些相关的槽位,这样就不会造成大面积的重复扫描。
使用Scan迭代哈希表时,有以下三种情况:
从迭代开始到结束,哈希表不 Rehash;
从迭代开始到结束,哈希表Rehash,但每次迭代,哈希表要么不开始 Rehash,要么已经结束 Rehash;
从一次迭代开始到结束,哈希表在一次或多次迭代中 Rehash。
即再 Rehash 过程中,执行 Scan 命令,这时数据可能只迁移了一部分。
因此,游标的实现需要兼顾以上三种情况。上述三种情况下游标实现的要求如下:
第一种情况比较简单。假设redis的hash表大小为4,第一个游标为0,读取第一个bucket的数据,然后游标返回2,下次读取bucket 2 ,依次遍历。
第二种情况更复杂。假设redis的hash表大小为4,如果rehash后大小变成8。如果如上返回游标(即返回2),则显示下图:
假设bucket 0读取后返回到cursor 2,当客户端再次Scan cursor 2时,hash表已经被rehash,大小翻倍到8,redis计算一个key bucket如下:
hash(key)&(size-1)
即如果大小为4,hash(key)&11,如果大小为8,hash(key)&111。所以当size从4扩大到8时,2 号bucket中的原始数据会被分散到2 (010) 和 6 (110) 这两个 bucket中。
从二进制来看,size为4时,在hash(key)之后,取低两位,即hash(key)&11,如果size为8,bucket位置为hash(key) & 111,即取低三个位。
所以依旧不会出现漏掉数据的情况。
第三种情况,如果返回游标2时正在进行rehash,则Hash表1的bucket 2中的一些数据可能已经rehash到了的Hash表2 的bucket[2]或bucket[6],那么必须完全遍历 哈希表2的 bucket 2 和 6,否则可能会丢失数据。
Redis 全局有两个Hash表,扩容时会渐进式的将表1的数据迁移到表2,查询时程序会先在 ht[0] 里面进行查找, 如果没找到的话, 就会继续到 ht[1] 里面进行查找。
具体游标计算代码如下:
Scan 命令中的游标,其实就是 Redis 内部的 bucket。
v = rev(v);
v++;
v = rev(v);
//下面将v的每一位倒过来再加1,再倒回去,这是什么意思呢,
//其实就是要将有效二进制位里面的高位第一个0位设置置为1,因为现在是0嘛
return v;代码逻辑非常简单,计算过程如下: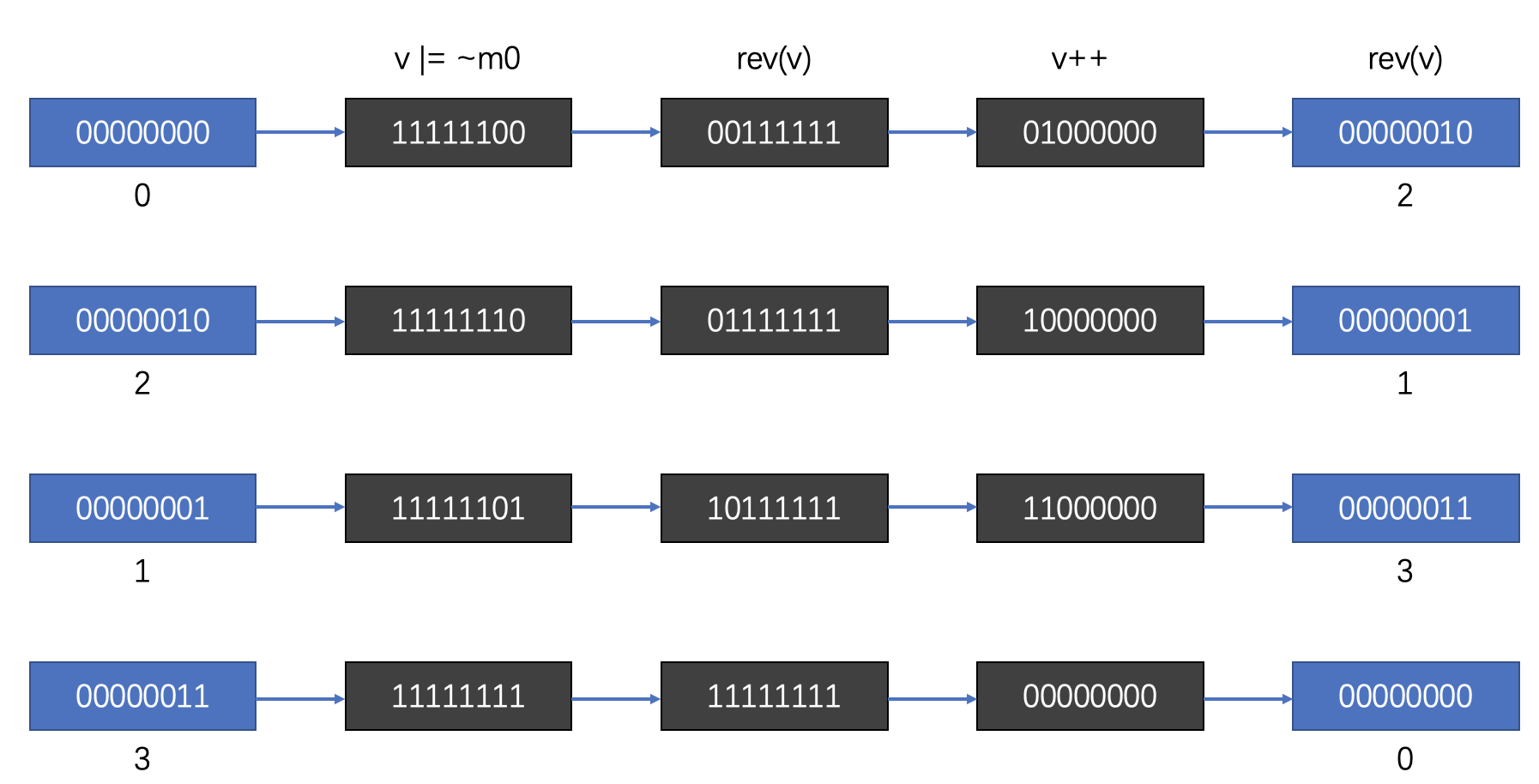
大小为 4 时,游标状态转换为 0-2-1-3。
当大小为 8 时,游标状态转换为 0-4-2-6-1-5-3-7
可以看出,当size由小变大时,所有原来的游标都能在大hashTable中找到对应的位置,并且顺序一致,不会遗漏数据。
缩容处理
之所以会出现重复数据,其实就是为了保证扩缩容后数据不丢。
假设当前 hash 大小为 8:
1)第一次先遍历了 0 号槽,返回游标为 4;
2)准备遍历 4 号槽,然后此时发生了缩容,4 号槽的元素也进到 0 号槽了。
3)但是0 号槽之前已经被遍历过了,此时会丢数据吗?
答案就在源码中:
do {
//扫描大点的表里面的槽位,注意这里是个循环,会将小表没有覆盖的slot全部扫描一次的
/* Emit entries at cursor */
de = t1->table[v & m1];
while (de) {
fn(privdata, de);
de = de->next;
}
/* Increment bits not covered by the smaller mask */
//下面的意思是,还需要扩展小点的表,将其后缀固定,然后看高位可以怎么扩充。
//其实就是想扫描一下小表里面的元素可能会扩充到哪些地方,需要将那些地方处理一遍。
//后面的(v & m0)是保留v在小表里面的后缀。
//((v | m0) + 1) & ~m0) 是想给v的扩展部分的二进制位不断的加1,来造成高位不断增加的效果。
v = (((v | m0) + 1) & ~m0) | (v & m0);
/* Continue while bits covered by mask difference is non-zero */
} while (v & (m0 ^ m1));//终止条件是v的高位区别位没有1了,其实就是说到头了。具体计算方法:
v = (((v | m0) + 1) & ~m0) | (v & m0);
右边的下半部分是v,左边的上半部分是v。(v&m0) 取出v的低位,例如size=4时v&00000011
左半边(v|m0) + 1 将V 的低位设置为1,然后+1 将进位到v 的高位,再次&m0,V 的高位将被取出。
假设游标返回2并且正在rehashing,大小从4变为8,那么M0 = 00000011 v = 00000010
根据公式计算的下一个光标是 ((00000010 | 00000011) +1) & (11111111100) | (00000010 & 00000011) = (00000100) & (11111111100) | (00000000010) = (000000000110) 正好是 6。
总结
Scan Count 参数限制的是遍历的 bucket 数,而不是限制的返回的元素个数
由于不同 bucket 中的元素个数不同,其中满足条件的个数也不同,所以每次 Scan 返回元素也不一定相同
Count 越大,Scan 总耗时越短,但是单次耗时越大,即阻塞Redis 时间边长
推荐 Count 大小为 1W左右
当 Count = Redis Key 总数时,Scan 和 Keys 效果一致
Scan 采用 逆二进制迭代法来计算游标,主要为了兼容Rehash的情况
Scan 为了兼容缩容后不漏掉数据,会出现重复遍历。
即客户端需要做去重处理
核心就是 逆二进制迭代法,比较复杂,而且算法作者也没有具体证明,为什么这样就能实现,只是测试发现没有问题,各种情况都能兼容。
具体算法细节可以看一下这个Github 相关讨论




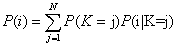

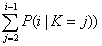
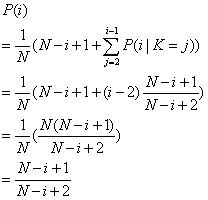


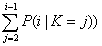 并不包括第j个乘客,所以不用考虑这个影响。对于第2~i-1个乘客而言,如果第j个乘客无论是坐在1还是j,他们都可以坐在自己的座位上,对他们来说没有区别,对他们的概率也没有任何影响。因此,这个变换是安全的。
并不包括第j个乘客,所以不用考虑这个影响。对于第2~i-1个乘客而言,如果第j个乘客无论是坐在1还是j,他们都可以坐在自己的座位上,对他们来说没有区别,对他们的概率也没有任何影响。因此,这个变换是安全的。
