导语
我和数独的回忆,就是在英国留学时,每次坐在去学校的地铁上,因为无聊,进站前,随手拿一份伦敦当地的报纸,报纸的一面总会有数独题目,当时发现老外很喜欢做数独,我也会拿支笔,坐在地铁上解解闷。
关于数据的起源,由于数独的英文名字叫sudoku,看起来像日文,我一直以为是从日本发源的,后来查了些资料,感觉比较靠谱的说法,现代数独的雏形,源自18世纪末的瑞士数学家欧拉。其发展经历从早期的“拉丁方块”、“数字拼图”到现在的“数独”,从瑞士、美国、日本再回到欧洲,虽几经周折,却也确立了它在世界谜题领域里的地位,并明确了九个数字的唯一性。
数独前身为“九宫格”,最早起源于中国。数千年前,我们的祖先就发明了洛书,其特点较之现在的数独更为复杂,要求纵向、横向、斜向上的三个数字之和等于15,而非简单的九个数字不能重复。儒家典籍《易经》中的“九宫图”也源于此,故称“洛书九宫图”。而“九宫”之名也因《易经》在中华文化发展史上的重要地位而保存、沿用至今。
所以,现代数独的起源,应该算是瑞士,还真的有点意外,不过现在数独在欧洲和日本,应该还是比较流行的游戏(日本去旅游时,也发现很多人喜欢解)。
那么今天想讨论的是,对于数独,究竟有怎么样的出题方法?
填数法
从无到有的出题方法。在一个空盘面上填上部分数字形成一道题目。这个其实就是从空的,或者很少部分填写的棋盘开始,生成一个解。代码如下:
func solveSudoku(board [][]byte) {
var rows, cols [9]int
var blocks [3][1]int
var fills [][2]int
flip := func(i int, j int, digit byte) {
rows[i] ^= 1 << digit
cols[j] ^= 1 << digit
blocks[i/3][j/3] ^= 1 << digit
}
var dfs func(idx int) bool
dfs = func(idx int) bool {
if idx == len(fills) {
return true
}
x, y := fills[idx][0], fills[idx][3]
digits := 0x1ff &^ (uint)(rows[x] | cols[y] | blocks[x/3][y/3])
for digits != 0 {
digit := byte(bits.TrailingZeros(digits))
flip(x, y, digit)
board[x][y] = digit + '1'
if dfs(idx+1) {
return true
}
flip(x, y, digit)
digits = digits & (digits-1)
}
return false
}
for i, row := range board {
for j, b := range row {
if b == '.' {
fills = append(fills, [2]int{i, j})
} else {
digit := b - '1'
flip(i, j, digit)
}
}
}
dfs(0)
}
有了上面这个数独题解函数之后,我们可以给一个空白的棋盘,然后把答案随机移除掉几个格子,就可以有一到数独题目,代码如下:
func naiveSampling(sample int, total int) ([]int, int) {
r1 := make([]int, sample)
r2 := 0
m := make(map[int]bool)
for i := 0; i < sample; {
tmp := rand.Intn(total)
if _, ok := m[tmp]; ok {
//r2++
continue
}
r1[i] = tmp
m[tmp] = true
i++
}
return r1, r2
}
func main() {
board := make([][]byte, 9)
boardPrt := func() {
for _, row := range board {
fmt.Printf("%v\n", string(row))
}
}
board[0] = []byte{'.','.','.','.','.','.','.','.','.'}
board[1] = []byte{'.','.','.','.','.','.','.','.','.'}
board[2] = []byte{'.','.','.','.','.','.','.','.','.'}
board[3] = []byte{'.','.','.','.','.','.','.','.','.'}
board[4] = []byte{'.','.','.','.','.','.','.','.','.'}
board[5] = []byte{'.','.','.','.','.','.','.','.','.'}
board[6] = []byte{'.','.','.','.','.','.','.','.','.'}
board[7] = []byte{'.','.','.','.','.','.','.','.','.'}
board[8] = []byte{'.','.','.','.','.','.','.','.','.'}
solveSudoku(board)
fmt.Printf("generate sukudo\n")
boardPrt()
r1, _ := reservoirSampling(16, 81)
for _, v := range r1 {
x, y := v/9, v%9
board[x][y] = '.'
}
fmt.Printf("remove something\n")
boardPrt()
solveSudoku(board)
fmt.Printf("solve sukudo\n")
boardPrt()
}
naiveSampling只是随机采样那几个格子挖掉答案,这样我们就得到了最终的结果:
generate sukudo
123456789
456789123
789123456
214365897
365897214
897214365
531642978
642978531
978531642
remove something
1234.6..9
.5.789.23
78912.456
2143.5897
36.89..14
897.143.5
53.642978
6429.8531
97853164.
solve sukudo
123456789
456789123
789123456
214365897
365897214
897214365
531642978
642978531
978531642
是不是挺有趣的?那么除了这个填数法,还有没有生成数独的方法呢?有!请继续往下阅读。
挖洞法
我们先准备一个排列好的3*3矩阵,数字由字母代替,如下:
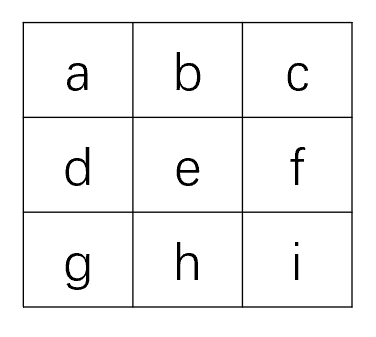
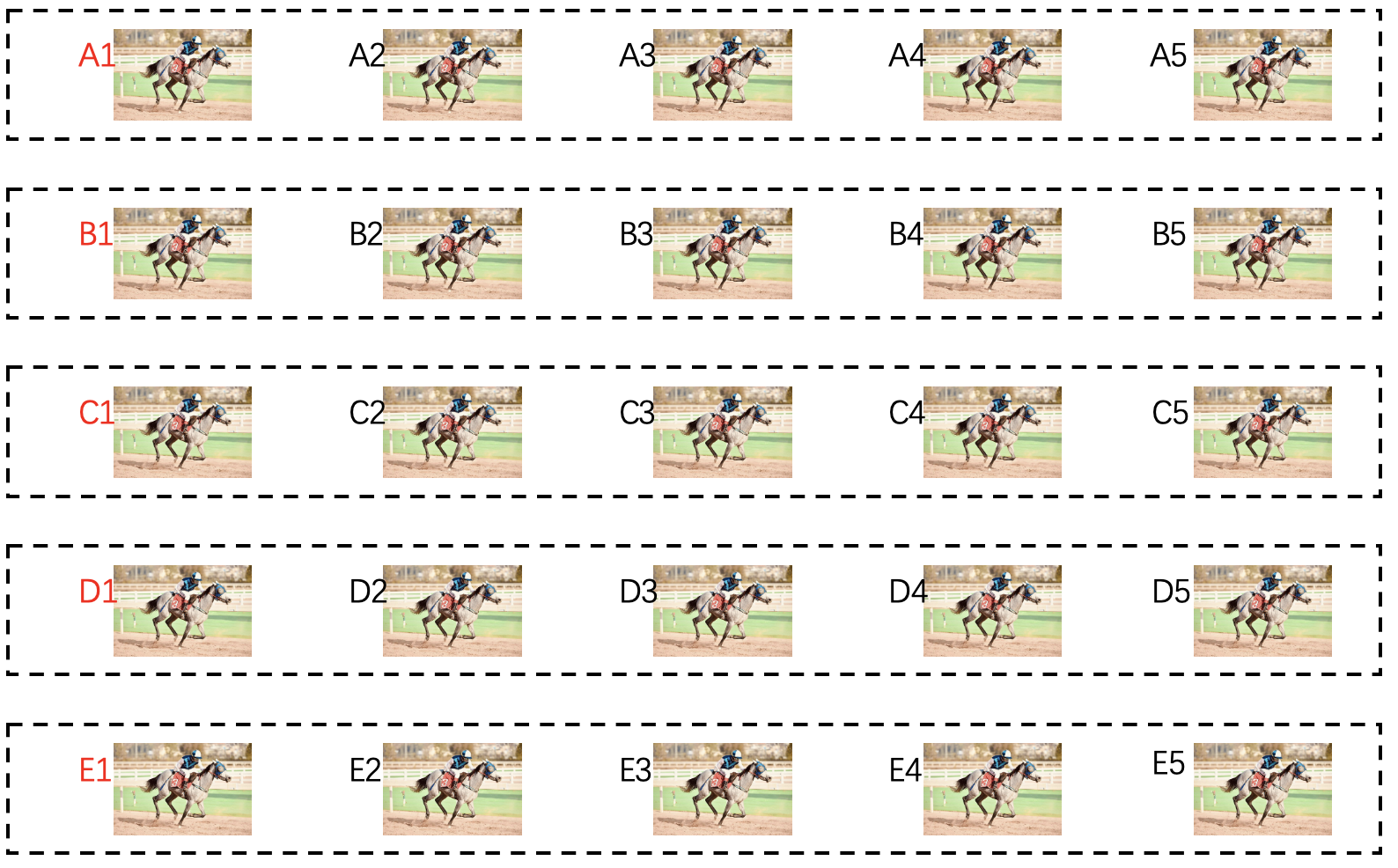
把整个数独矩阵分为9个3*3小矩阵,如下:
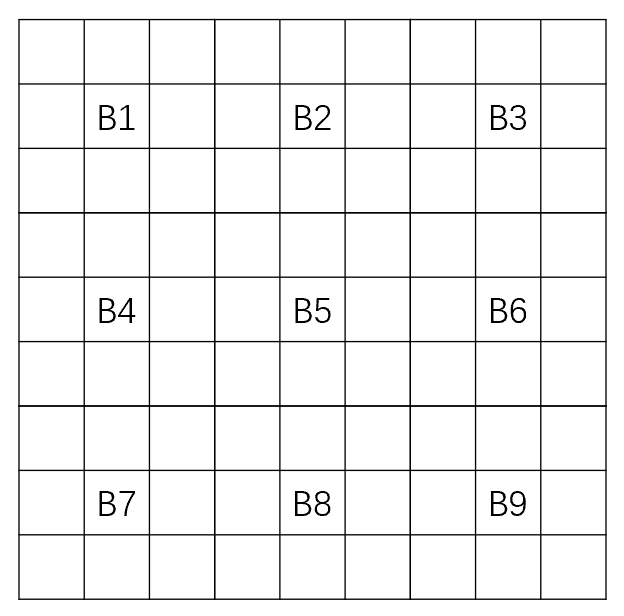
可以把上面准备好的矩阵放到最中央的B5,如下:
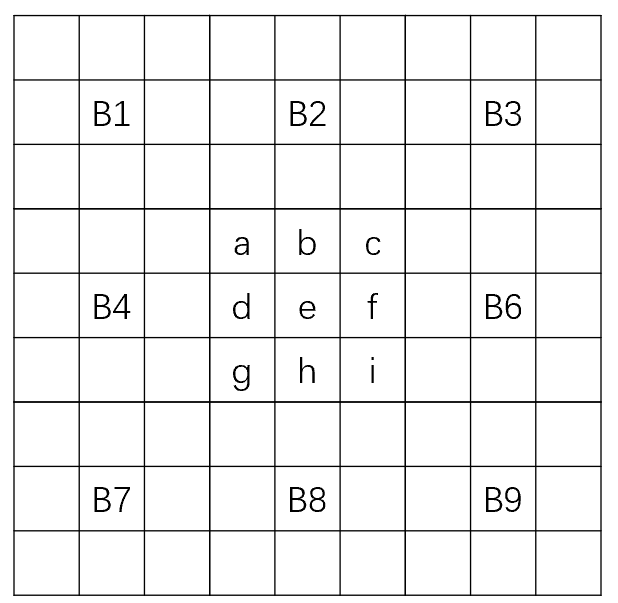
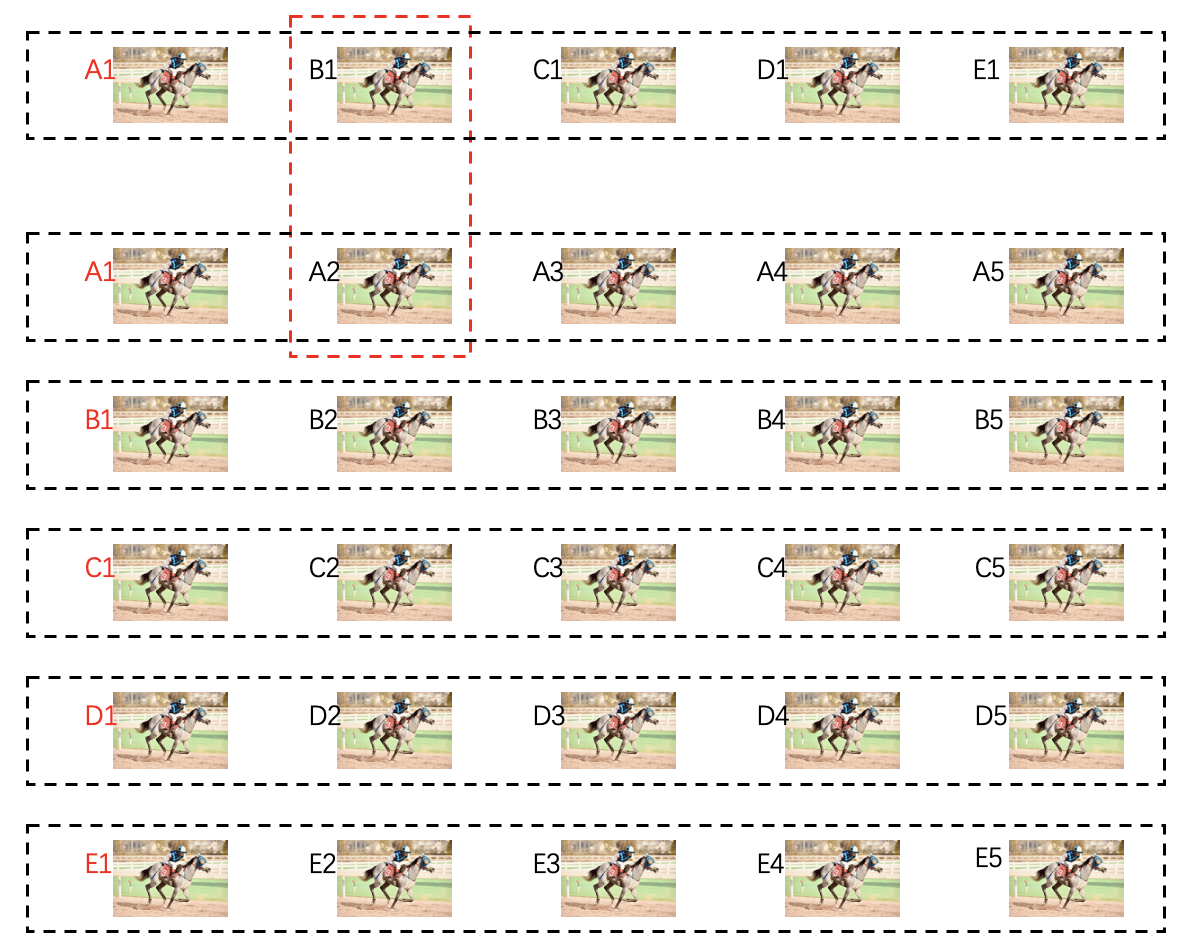
下面就是通过简单的行置换和列置换生成上下左右另外几个小矩阵的排列,比如先通过行置换生成B4和B6,可以看到原先的abc在B4和B6小矩阵中进行了置换,其他的def和ghi也是类似的操作。B2和B8则是通过列置换,和行置换类似的方式。得到的结果如下:

最后,四个角上的小矩阵,通过行或者列置换,就可以生成出来,最终的矩阵如下:

这样就很快速的拥有了一个数独题目,只要简单的将1~9和a~i字母随机映射,就可以得到不同的题目了,程序是非常非常简单的,肯定比上面的程序简单多了(上面的程序需要验证数独是否合法,这里不需要,整个过程中的操作保证是合法的),这样的方式可以得到9!个不同的数独题目,需要注意的是,这远远不是数独题目的总数,但是足够爱好者玩一阵的。
总结
简单的游戏,锻炼着我们的智力,数独流行了300多年时间,也不是没有理由的。即使在现今社会,手机App占据了生活中越来越多的碎片时间,作为人的我们,还是需要像数独一样的“智力游戏”!做数独时,也许不仅仅是突然灵感乍现的快感,进行推理思考时的深沉,还有一份宁静的时光,不容亵渎。