如何给磁盘文件排序?
如何给磁盘文件排序?
近来,翻出来之前买的《编程珠玑》,买来还没有仔细阅读,随手翻开看看,经典书籍果然是经典书籍,读起来,还是那么深刻。我准备将自己对书上内容的理解记录下来,一是通过整理巩固知识,二是写成文字,可作为输出内容。
上来讲的是“如何给磁盘文件排序”的问题,问题的准确描述如下:
输入:一个最多包含n个正整数的文件,每个数都小于n,其中n=10^7。如果在输入文件中有任何整数重复出现就是致命错误。没有其他数据与该整数相关联。
输出:按升序排列输入整数的列表。
约束:最多有(大约)1MB的内存空间可以使用,有充足的磁盘存储空间可用。运行时间最多为几分钟(感觉到之前时代算力的紧张了),运行时间为10秒就不需要优化了。(现在可以改为运行时间低于100ms就不需要优化了)。
思考过程:
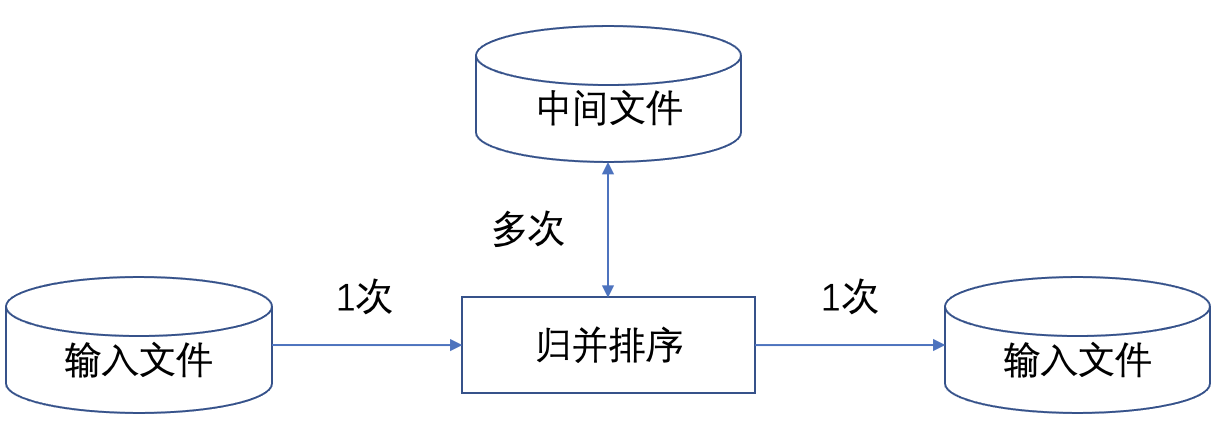
方法一、归并排序读入输入文件一次,然后在中间文件的协作下,完成多路归并排序,并写入输出文件一次。中间文件需要多次读写。
方法二、40趟算法读入输入文件,前提是要知道整数分布的范围,那么就可以按号段去扫描读入,比如问题中描述的1MB空间,如果用来存0~100万数字表述的号码,那么一个号码可以使用一个32位整型数表示,1MB空间可以存大约250000个号码,100万的号码可以先扫描到内存中0~249999之间的整数,内存做快速排序,结果存到输出文件,以此类推。

下图所示的方案更可取。我们结合上述两种方法的优点,读输入文件仅一次,且不使用任何中间文件。但前提是1MB内存需要来表示所有的整数。该怎么做呢?

解决方案:
现在想来,直接的方案就是使用bitmap,举例,可以使用一个20位长的字符串表示一个所有元素都小于20的简单的非负整数集合。例如,可以使用如下字符串(二进制的表示)来表示集合{1,2,3,5,8,13}:
0 1 1 1 0 1 0 0 1 0 0 0 0 1 0 0 0 0 0 0
那么1MB内存有3000万bit,每个bit表示1个整形数,可以表示的整数个数可以达到3000+万。这种表示利用了该问题的三个在排序问题中不常见的属性:输入数据限制在相对较小的范围内;数据没有重复;而且对每条记录而言,除了单一整数外,没有任何其他关联数据。
实现代码:
#include <time.h>
#include <vector>
#include <algorithm>
#include <string>
#include <fstream>
using namespace std;
#define BITSPERWORD 32
#define SHIFT 5
#define MASK 0x1F
#define N 10000000
int a[1+N/BITSPERWORD];
void set(int i) { a[i>>SHIFT] |= (1<<(i & MASK)); }
void clr(int i) { a[i>>SHIFT] &= ~(1<<(i & MASK)); }
int test(int i) { return a[i>>SHIFT] & (1<<(i & MASK)); }
unsigned long GetTickCount()
{
struct timespec ts;
clock_gettime(CLOCK_MONOTONIC, &ts);
return (ts.tv_sec * 1000 + ts.tv_nsec / 1000000);
}
void stl_sort() {
vector<int> v;
ifstream ifile;
ifile.open("./input.txt");
string line;
unsigned long begin_time = GetTickCount();
while(getline(ifile, line)) {
v.push_back(atoi(line.c_str()));
}
unsigned long end_time = GetTickCount();
printf("finish input, cost time=%d\n", end_time-begin_time);
ifile.close();
begin_time = GetTickCount();
sort(v.begin(), v.end());
end_time = GetTickCount();
printf("finish sorting, cost time=%d\n", end_time-begin_time);
ofstream ofile;
ofile.open("./output1.txt");
begin_time = GetTickCount();
for (int i = 0; i < v.size(); ++i) {
ofile << v[i] << endl;
}
end_time = GetTickCount();
printf("finish writing, cost time=%d\n", end_time-begin_time);
ofile.close();
}
void bitmap_sort() {
vector<int> v;
ifstream ifile;
ifile.open("./input.txt");
string line;
unsigned long begin_time = GetTickCount();
while(getline(ifile, line)) {
v.push_back(atoi(line.c_str()));
}
unsigned long end_time = GetTickCount();
printf("finish input, cost time=%d\n", end_time-begin_time);
ifile.close();
begin_time = GetTickCount();
for (int i = 0; i <= N; ++i) {
clr(i);
}
for (int i = 0; i < v.size(); ++i) {
//printf("set: i=%d, v[i]=%d\n", i, v[i]);
set(v[i]);
}
end_time = GetTickCount();
printf("finish sorting, cost time=%d\n", end_time-begin_time);
ofstream ofile;
ofile.open("./output2.txt");
begin_time = GetTickCount();
for (int i = 0; i <= N; ++i) {
if (test(i)) {
ofile << i << endl;
}
}
end_time = GetTickCount();
printf("finish writing, cost time=%d\n", end_time-begin_time);
ofile.close();
}
上面代码实现了从文件读入数据,排序(STL实现的排序和bitmap方式),实测在1000万量级上的耗时如下:
finish input, cost time=795
finish sorting, cost time=3873 // 3873ms
finish writing, cost time=13634
finish input, cost time=793
finish sorting, cost time=151 // 151ms
finish writing, cost time=8777
排序的加速效果是非常明显的,同样数据规模,比STL实现的排序算法加速了20x。
另外,这个bitmap表示一个整数集合的思想,也不仅仅用在排序场景中,有些去重的场景也适用(或者检查有无重复项),比如今天遇到的leetcode上一道题目,题目不难,但是如果使用bitmap实现,代码挺整洁的。
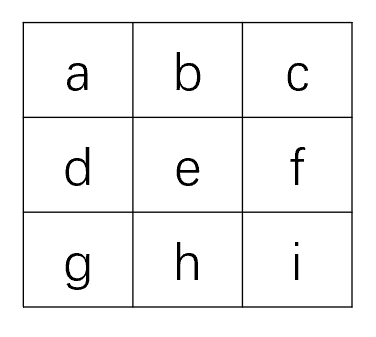
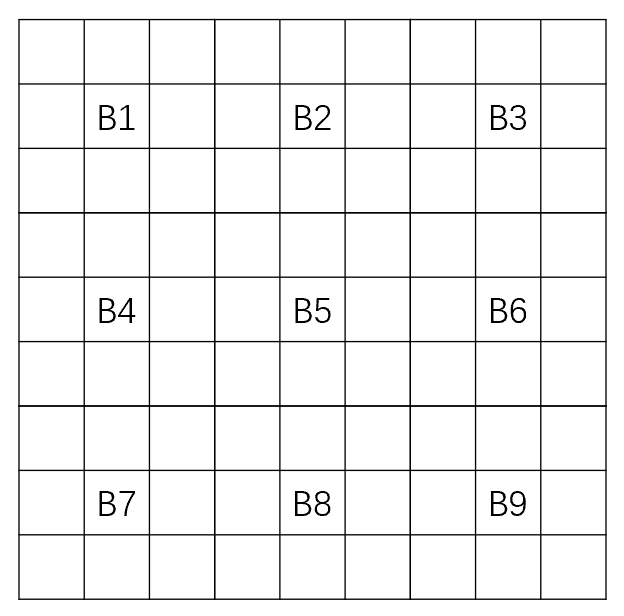
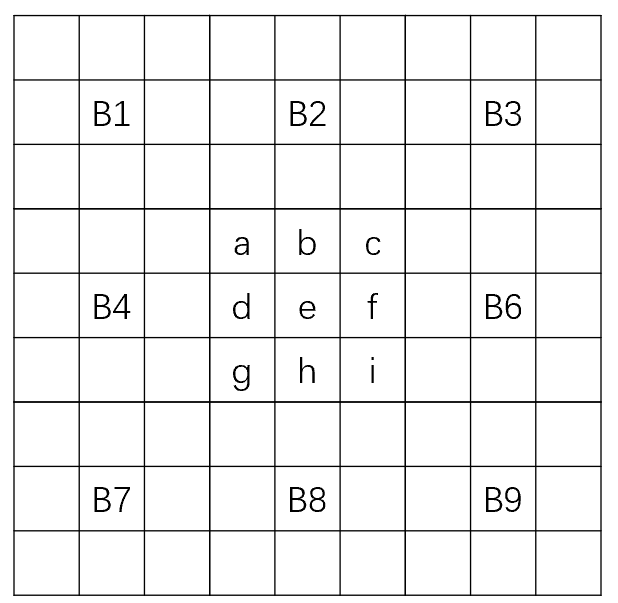
检查是否每一行每一列都包含全部整数