导语
函数式编程的中非常重要的Map、Reduce、Filter的三种操作,这三种操作可以让我们非常方便灵活地进行一些数据处理——我们的程序中大多数情况下都是在到倒腾数据,尤其对于一些需要统计的业务场景,Map/Reduce/Filter是非常通用的玩法。
例子
Map示例
下面的程序代码中,我们写了两个Map函数,这两个函数需要两个参数:
- 一个是字符串数组 []string,说明需要处理的数据一个字符串
- 另一个是一个函数func(s string) string 或 func(s string) int
func MapStrToStr(arr []string, fn func(s string) string) []string {
var newArray = []string{}
for _, it := range arr {
newArray = append(newArray, fn(it))
}
return newArray
}
func MapStrToInt(arr []string, fn func(s string) int) []int {
var newArray = []int{}
for _, it := range arr {
newArray = append(newArray, fn(it))
}
return newArray
}
整个Map函数运行逻辑都很相似,函数体都是在遍历第一个参数的数组,然后,调用第二个参数的函数,然后把其值组合成另一个数组返回。
于是我们就可以这样使用这两个函数:
var list = []string{"Hao", "Chen", "MegaEase"}
x := MapStrToStr(list, func(s string) string {
return strings.ToUpper(s)
})
fmt.Printf("%v\n", x)
//["HAO", "CHEN", "MEGAEASE"]
y := MapStrToInt(list, func(s string) int {
return len(s)
})
fmt.Printf("%v\n", y)
//[3, 4, 8]
我们可以看到,我们给第一个 MapStrToStr() 传了函数做的是 转大写,于是出来的数组就成了全大写的,给MapStrToInt() 传的是算其长度,所以出来的数组是每个字符串的长度。
我们再来看一下Reduce和Filter的函数是什么样的。
Reduce示例
func Filter(arr []int, fn func(n int) bool) []int {
var newArray = []int{}
for _, it := range arr {
if fn(it) {
newArray = append(newArray, it)
}
}
return newArray
}
var intset = []int{1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
out := Filter(intset, func(n int) bool {
return n%2 == 1
})
fmt.Printf("%v\n", out)
out = Filter(intset, func(n int) bool {
return n > 5
})
fmt.Printf("%v\n", out)
Filter示例
func Filter(arr []int, fn func(n int) bool) []int {
var newArray = []int{}
for _, it := range arr {
if fn(it) {
newArray = append(newArray, it)
}
}
return newArray
}
var intset = []int{1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
out := Filter(intset, func(n int) bool {
return n%2 == 1
})
fmt.Printf("%v\n", out)
out = Filter(intset, func(n int) bool {
return n > 5
})
fmt.Printf("%v\n", out)
下图是一个比喻,其非常形象地说明了Map-Reduce是的业务语义,其在数据处理中非常有用。
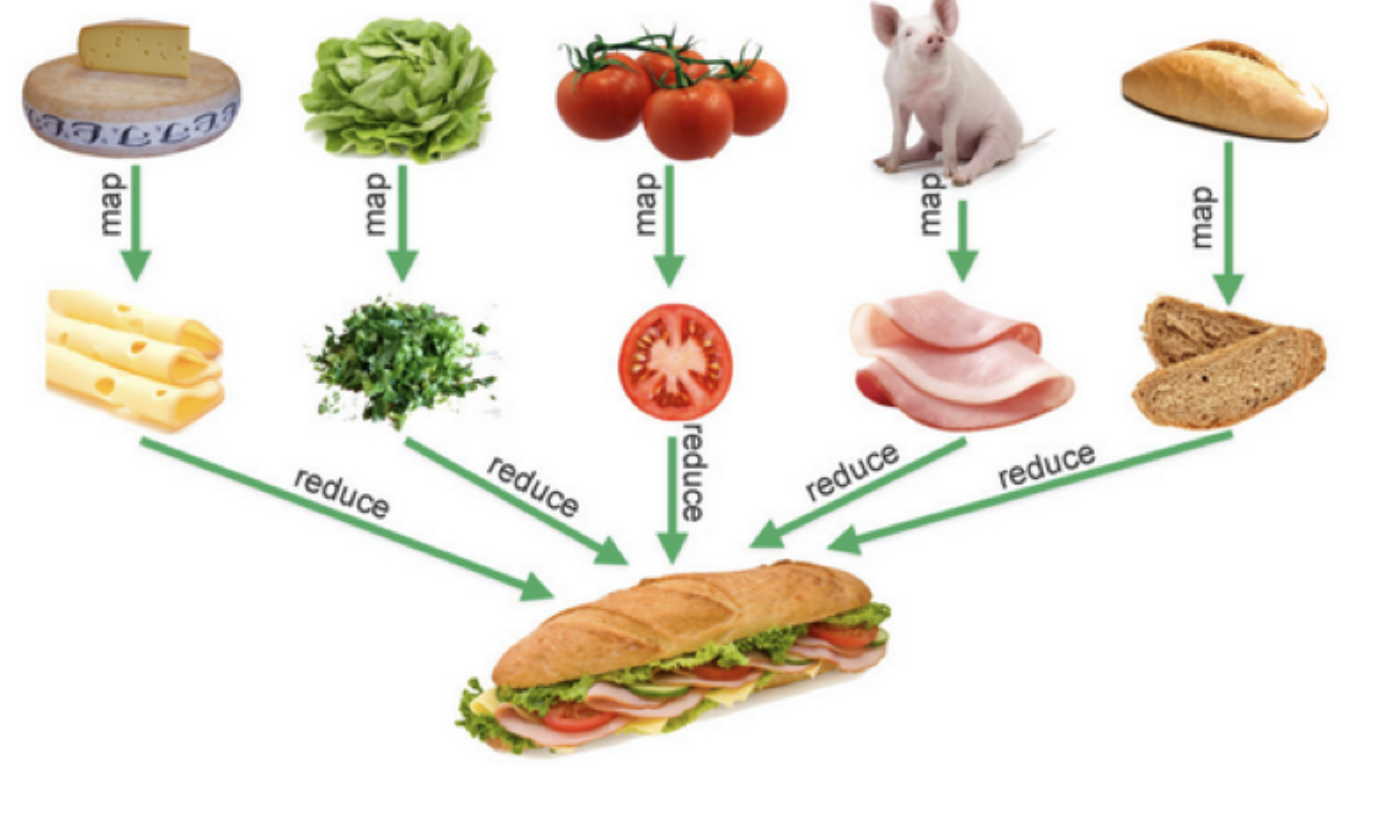
业务示例
通过上面的一些示例,你可能有一些明白,Map/Reduce/Filter只是一种控制逻辑,真正的业务逻辑是在传给他们的数据和那个函数来定义的。是的,这是一个很经典的“业务逻辑”和“控制逻辑”分离解耦的编程模式。下面我们来看一个有业务意义的代码,来让大家强化理解一下什么叫“控制逻辑”与业务逻辑分离。
首先,我们一个员工对象,以及一些数据。
type Employee struct {
Name string
Age int
Vacation int
Salary int
}
var list = []Employee{
{"Hao", 44, 0, 8000},
{"Bob", 34, 10, 5000},
{"Alice", 23, 5, 9000},
{"Jack", 26, 0, 4000},
{"Tom", 48, 9, 7500},
{"Marry", 29, 0, 6000},
{"Mike", 32, 8, 4000},
}
相关的Reduce/Fitler函数:
func EmployeeCountIf(list []Employee, fn func(e *Employee) bool) int {
count := 0
for i, _ := range list {
if fn(&list[i]) {
count += 1
}
}
return count
}
func EmployeeFilterIn(list []Employee, fn func(e *Employee) bool) []Employee {
var newList []Employee
for i, _ := range list {
if fn(&list[i]) {
newList = append(newList, list[i])
}
}
return newList
}
func EmployeeSumIf(list []Employee, fn func(e *Employee) int) int {
var sum = 0
for i, _ := range list {
sum += fn(&list[i])
}
return sum
}
简单说明一下:
- EmployeeConutIf 和 EmployeeSumIf 分别用于统满足某个条件的个数或总数。它们都是Filter +
Reduce的语义。 - EmployeeFilterIn 就是按某种条件过虑。就是Fitler的语义。
于是我们就可以有如下的代码。
统计有多少员工大于40岁
old := EmployeeCountIf(list, func(e *Employee) bool {
return e.Age > 40
})
fmt.Printf("old people: %d\n", old)
统计有多少员工薪水大于6000
high_pay := EmployeeCountIf(list, func(e *Employee) bool {
return e.Salary >= 6000
})
fmt.Printf("High Salary people: %d\n", high_pay)
//High Salary people: 4
列出有没有休假的员工
no_vacation := EmployeeFilterIn(list, func(e *Employee) bool {
return e.Vacation == 0
})
fmt.Printf("People no vacation: %v\n", no_vacation)
//People no vacation: [{Hao 44 0 8000} {Jack 26 0 4000} {Marry 29 0 6000}]
统计所有员工的薪资总和
total_pay := EmployeeSumIf(list, func(e *Employee) int {
return e.Salary
})
fmt.Printf("Total Salary: %d\n", total_pay)
//Total Salary: 43500
统计30岁以下员工的薪资总和
younger_pay := EmployeeSumIf(list, func(e *Employee) int {
if e.Age < 30 {
return e.Salary
}
return 0 })
泛型Map-Reduce
我们可以看到,上面的Map-Reduce都因为要处理数据的类型不同而需要写出不同版本的Map-Reduce,虽然他们的代码看上去是很类似的。所以,这里就要带出来泛型编程了,Go语言在本文写作的时候还不支持泛型(注:Go开发团队技术负责人Russ Cox在2012年11月21golang-dev上的mail确认了Go泛型(type parameter)将在Go 1.18版本落地,即2022.2月份)。
简单版 Generic Map
所以,目前的Go语言的泛型只能用 interface{} + reflect来完成,interface{} 可以理解为C中的 void*,Java中的 Object ,reflect是Go的反射机制包,用于在运行时检查类型。
下面我们来看一下一个非常简单不作任何类型检查的泛型的Map函数怎么写。
func Map(data interface{}, fn interface{}) []interface{} {
vfn := reflect.ValueOf(fn)
vdata := reflect.ValueOf(data)
result := make([]interface{}, vdata.Len())
for i := 0; i < vdata.Len(); i++ {
result[i] = vfn.Call([]reflect.Value{vdata.Index(i)})[0].Interface()
}
return result
}
上面的代码中
- 通过 reflect.ValueOf() 来获得 interface{} 的值,其中一个是数据 vdata,另一个是函数 vfn;
- 然后通过 vfn.Call() 方法来调用函数,通过 []refelct.Value{vdata.Index(i)}来获得数据。
Go语言中的反射的语法还是有点令人费解的,但是简单看一下手册还是能够读懂的。我这篇文章不讲反射,所以相关的基础知识还请大家自行Google相关的教程。
于是,我们就可以有下面的代码——不同类型的数据可以使用相同逻辑的Map()代码。
square := func(x int) int {
return x * x
}
nums := []int{1, 2, 3, 4}
squared_arr := Map(nums,square)
fmt.Println(squared_arr)
//[1 4 9 16]
upcase := func(s string) string {
return strings.ToUpper(s)
}
strs := []string{"Hao", "Chen", "MegaEase"}
upstrs := Map(strs, upcase);
fmt.Println(upstrs)
//[HAO CHEN MEGAEASE]
但是因为反射是运行时的事,所以,如果类型什么出问题的话,就会有运行时的错误。比如:
x := Map(5, 5)
fmt.Println(x)
上面的代码可以很轻松的编译通过,但是在运行时就出问题了,还是panic错误……
panic: reflect: call of reflect.Value.Len on int Value
goroutine 1 [running]:
reflect.Value.Len(0x10b5240, 0x10eeb58, 0x82, 0x10716bc)
/usr/local/Cellar/go/1.15.3/libexec/src/reflect/value.go:1162 +0x185
main.Map(0x10b5240, 0x10eeb58, 0x10b5240, 0x10eeb60, 0x1, 0x14, 0x0)
/Users/chenhao/.../map.go:12 +0x16b
main.main()
/Users/chenhao/.../map.go:42 +0x465
exit status 2
健壮版的Generic Map
所以,如果要写一个健壮的程序,对于这种用interface{} 的“过度泛型”,就需要我们自己来做类型检查。下面是一个有类型检查的Map代码:
func Transform(slice, function interface{}) interface{} {
return transform(slice, function, false)
}
func TransformInPlace(slice, function interface{}) interface{} {
return transform(slice, function, true)
}
func transform(slice, function interface{}, inPlace bool) interface{} {
//check the <code data-enlighter-language="raw" class="EnlighterJSRAW">slice</code> type is Slice
sliceInType := reflect.ValueOf(slice)
if sliceInType.Kind() != reflect.Slice {
panic("transform: not slice")
}
//check the function signature
fn := reflect.ValueOf(function)
elemType := sliceInType.Type().Elem()
if !verifyFuncSignature(fn, elemType, nil) {
panic("trasform: function must be of type func(" + sliceInType.Type().Elem().String() + ") outputElemType")
}
sliceOutType := sliceInType
if !inPlace {
sliceOutType = reflect.MakeSlice(reflect.SliceOf(fn.Type().Out(0)), sliceInType.Len(), sliceInType.Len())
}
for i := 0; i < sliceInType.Len(); i++ {
sliceOutType.Index(i).Set(fn.Call([]reflect.Value{sliceInType.Index(i)})[0])
}
return sliceOutType.Interface()
}
func verifyFuncSignature(fn reflect.Value, types ...reflect.Type) bool {
//Check it is a funciton
if fn.Kind() != reflect.Func {
return false
}
// NumIn() - returns a function type's input parameter count.
// NumOut() - returns a function type's output parameter count.
if (fn.Type().NumIn() != len(types)-1) || (fn.Type().NumOut() != 1) {
return false
}
// In() - returns the type of a function type's i'th input parameter.
for i := 0; i < len(types)-1; i++ {
if fn.Type().In(i) != types[i] {
return false
}
}
// Out() - returns the type of a function type's i'th output parameter.
outType := types[len(types)-1]
if outType != nil && fn.Type().Out(0) != outType {
return false
}
return true
}
上面的代码一下子就复杂起来了,可见,复杂的代码都是在处理异常的地方。我不打算Walk through 所有的代码,别看代码多,但是还是可以读懂的,下面列几个代码中的要点:
- 代码中没有使用Map函数,因为和数据结构和关键有含义冲突的问题,所以使用Transform,这个来源于 C++ STL库中的命名。
- 有两个版本的函数,一个是返回一个全新的数组 – Transform(),一个是“就地完成” – TransformInPlace();
- 在主函数中,用 Kind() 方法检查了数据类型是不是 Slice,函数类型是不是Func;
- 检查函数的参数和返回类型是通过 verifyFuncSignature() 来完成的,其中:NumIn() – 用来检查函数的“入参”,NumOut() 用来检查函数的“返回值”;
- 如果需要新生成一个Slice,会使用 reflect.MakeSlice() 来完成。
好了,有了上面的这段代码,我们的代码就很可以很开心的使用了:
可以用于字符串数组:
list := []string{"1", "2", "3", "4", "5", "6"}
result := Transform(list, func(a string) string{
return a +a +a
})
//{"111","222","333","444","555","666"}
可以用于整形数组:
list := []int{1, 2, 3, 4, 5, 6, 7, 8, 9}
TransformInPlace(list, func (a int) int {
return a*3
})
//{3, 6, 9, 12, 15, 18, 21, 24, 27}
可以用于结构体:
var list = []Employee{
{"Hao", 44, 0, 8000},
{"Bob", 34, 10, 5000},
{"Alice", 23, 5, 9000},
{"Jack", 26, 0, 4000},
{"Tom", 48, 9, 7500},
}
result := TransformInPlace(list, func(e Employee) Employee {
e.Salary += 1000
e.Age += 1
return e
})
健壮版的 Generic Reduce
同样,泛型版的 Reduce 代码如下:
func Reduce(slice, pairFunc, zero interface{}) interface{} {
sliceInType := reflect.ValueOf(slice)
if sliceInType.Kind() != reflect.Slice {
panic("reduce: wrong type, not slice")
}
len := sliceInType.Len()
if len == 0 {
return zero
} else if len == 1 {
return sliceInType.Index(0)
}
elemType := sliceInType.Type().Elem()
fn := reflect.ValueOf(pairFunc)
if !verifyFuncSignature(fn, elemType, elemType, elemType) {
t := elemType.String()
panic("reduce: function must be of type func(" + t + ", " + t + ") " + t)
}
var ins [2]reflect.Value
ins[0] = sliceInType.Index(0)
ins[1] = sliceInType.Index(1)
out := fn.Call(ins[:])[0]
for i := 2; i < len; i++ {
ins[0] = out
ins[1] = sliceInType.Index(i)
out = fn.Call(ins[:])[0]
}
return out.Interface()
}
健壮版的 Generic Filter
同样,泛型版的 Filter 代码如下(同样分是否“就地计算”的两个版本):
func Filter(slice, function interface{}) interface{} {
result, _ := filter(slice, function, false)
return result
}
func FilterInPlace(slicePtr, function interface{}) {
in := reflect.ValueOf(slicePtr)
if in.Kind() != reflect.Ptr {
panic("FilterInPlace: wrong type, " +
"not a pointer to slice")
}
_, n := filter(in.Elem().Interface(), function, true)
in.Elem().SetLen(n)
}
var boolType = reflect.ValueOf(true).Type()
func filter(slice, function interface{}, inPlace bool) (interface{}, int) {
sliceInType := reflect.ValueOf(slice)
if sliceInType.Kind() != reflect.Slice {
panic("filter: wrong type, not a slice")
}
fn := reflect.ValueOf(function)
elemType := sliceInType.Type().Elem()
if !verifyFuncSignature(fn, elemType, boolType) {
panic("filter: function must be of type func(" + elemType.String() + ") bool")
}
var which []int
for i := 0; i < sliceInType.Len(); i++ {
if fn.Call([]reflect.Value{sliceInType.Index(i)})[0].Bool() {
which = append(which, i)
}
}
out := sliceInType
if !inPlace {
out = reflect.MakeSlice(sliceInType.Type(), len(which), len(which))
}
for i := range which {
out.Index(i).Set(sliceInType.Index(which[i]))
}
return out.Interface(), len(which)
}
后记
还有几个未尽事宜:
- 使用反射来做这些东西,会有一个问题,那就是代码的性能会很差。所以,上面的代码不能用于你需要高性能的地方。怎么解决这个问题,我们会在本系列文章的下一篇文章中讨论。
- 上面的代码大量的参考了 Rob Pike的版本,他的代码在 https://github.com/robpike/filter
- 其实,在全世界范围内,有大量的程序员都在问Go语言官方什么时候在标准库中支持 Map/Reduce,Rob Pike说,这种东西难写吗?还要我们官方来帮你们写么?这种代码我多少年前就写过了,但是,我从来一次都没有用过,我还是喜欢用“For循环”,我觉得你最好也跟我一起用“For循环”。
我个人觉得,Map/Reduce在数据处理的时候还是很有用的,Rob Pike可能平时也不怎么写“业务逻辑”的代码,所以,对他来说可能也不太了解业务的变化有多么的频繁……
当然,好还是不好,由你来判断,但多学一些编程模式是对自己的帮助也是很有帮助的。