上海疫情封在家中有三个月，辅导了小孩子功课，每每小孩遇到不会做的题目，比她更着急。有时也会想起自己学生时代的样子，遇到难题，心中升起必须克服难题的决心，现在自己娃，怎么没有我当年的风采了。哈哈，扯远了，这两天网上看到一道小学二年级的题目，其实我之前做过类似的题目，但是当下还是震惊了，怎么现在小学二年级题目有这么难？

题目是这样的：

配合网友的回复，我马上想到了之前类似的问题，说是25匹马，5个赛道，至少比几场保证找出最快的2匹马。赛马这题答案我记得很清楚7场比赛，先分组进行小组赛：

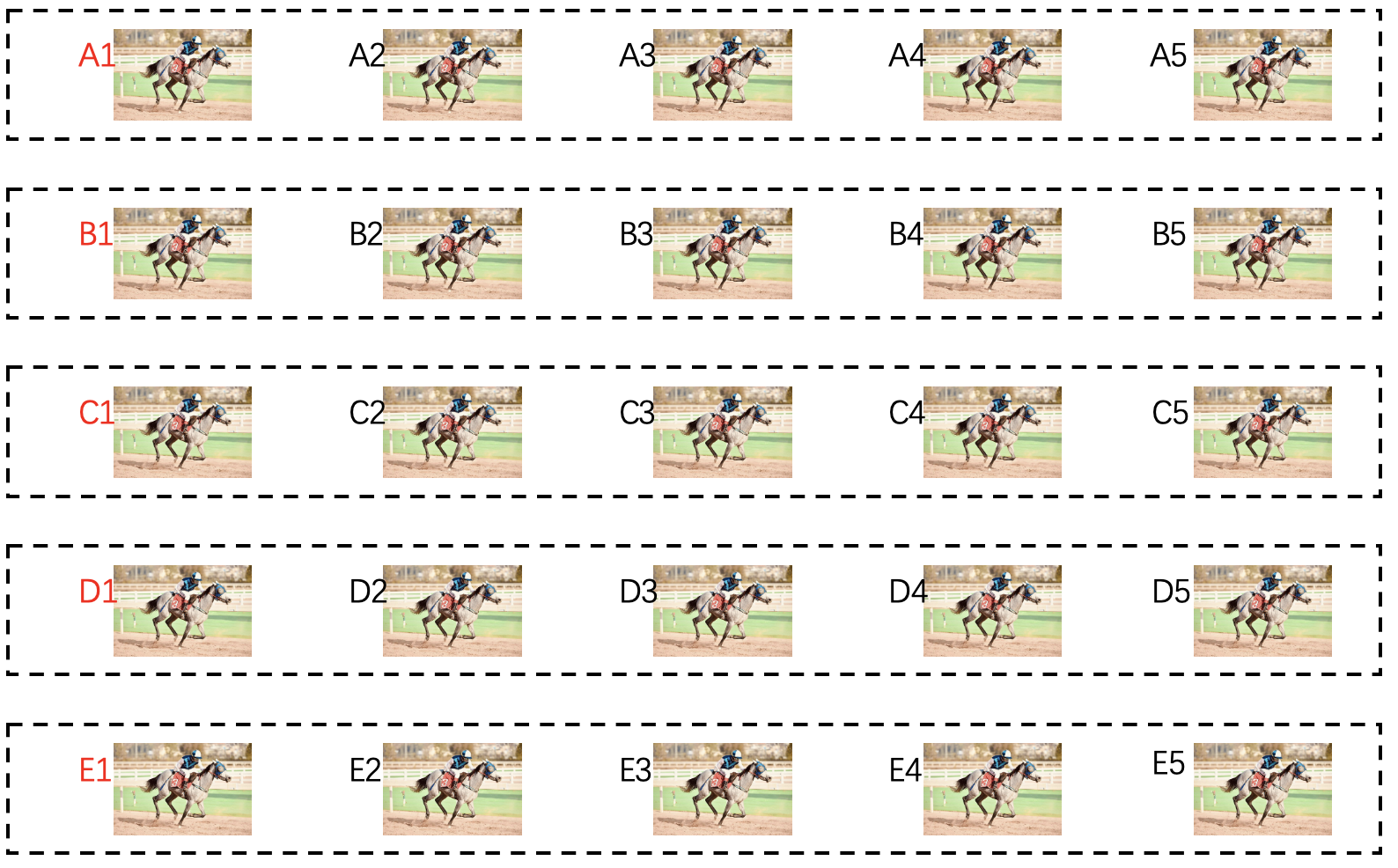
首先一个虚线框就是一场比赛，上来25匹马，分5组，进行5场预赛。5组比赛会得到组内的名次，比如A组，A1->A2->A3->A4->A5，每组第一名就是A1，B1，C1，D1和E1，然后第一名之间安排一场决赛：

假设结果就是A1->B1->C1->D1->E1(真正结果不重要，不管怎么样，总能推理出最后的结论)，这时候我们就通过4场比赛，知道了第一名是A1，那第二名是谁呢，是不是B1，不一定哦，有可能是在小组赛中被A1淘汰的A2，所以安排场附加赛吧，A2 vs B1：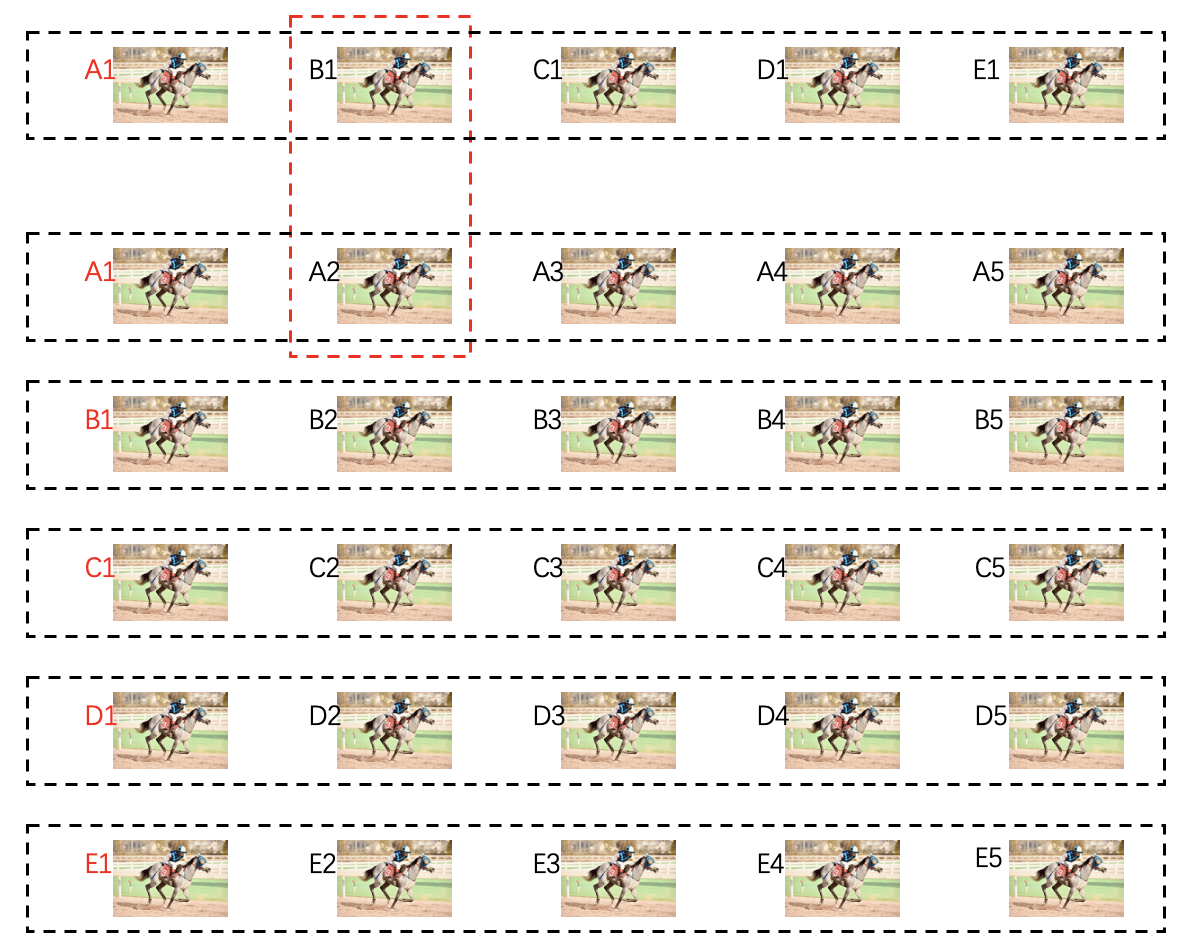

附加赛之后，就能知道前两名了。话说回小学二年级赛车这道题目，其实思路一模一样，就是通过小组赛->决赛->附加赛，完成前两名的确认，也就是说赛车的话，通过至少5场比赛，保证找出前两名的赛车。

作为小学二年级的题目很变态了吧，但是出题的人还多问了一句，怎么证明这件事情呢，为什么通过4场比赛一定不能保证找出前两名呢？这个证明难倒我了，抓耳挠腮半天，没想出来。然后我就看了下出题老师的分析，茅塞顿开，原来还可以使用图论+反正法来证明。大致的过程如下：
首先把每一辆赛车想象成点，那么我们一共有9辆赛车，一共9个点，每场比赛，只能进行3辆赛车的比拼，每次比拼完，我们会有一个名次，紧挨着的前后两名之间，使用一条有向边连接，这个我文字讲得有点绕口，一图解千愁：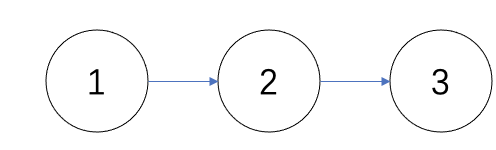

圆圈表示赛车，1号比2号快，2号比3号快，所以每次比赛，我们仅仅能得到2条有向边，如果进行4场比赛，那么总共的有向边数量是4*2 = 8条，而赛车的数量是9，也就是节点数量是9，8条边，9个点，如果要保证所有边都连接到一张图中，不能出现环，否则边的数量不够。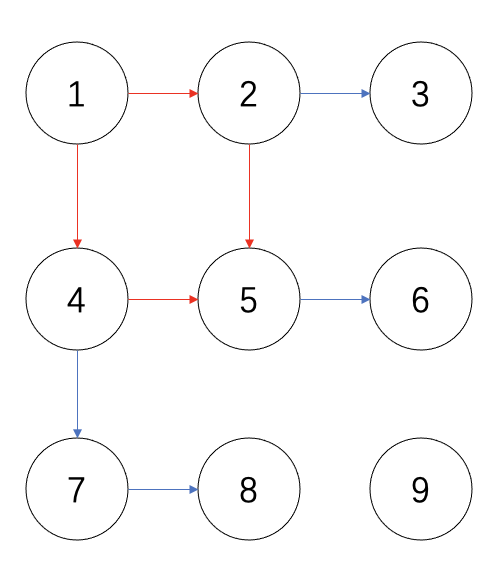

出现环就意味着9个点形成了若干个分开的子图，上面图中9个节点，分为了两个子图，那么就会有一个问题，第一名都不知道是谁，为什么？因为在1～8节点所在的图中，1号赛车最快，9号赛车单独成子图，9号赛车和谁都没有比过，那么到底9号和1号赛车谁快呢？不知道。所以8条边，安排的比赛结果，划分为多个子图，这样是无法确认前两名的。

那我们4场比赛的结果，如何是可以前两名的图形呢，如下：

左边就是分3场比赛（1、4、7，2、5、8和3、6、9分别比赛），得到结果后，4、2、3比一次，结果是4->2->3，转化这张单图，得到右侧的结果，其实就是一个树形的图，那么前两名就是1、4号赛车。

这样我们很容易举出反例，你不是就8条边么，我最后4、2、3的结果是2->4->3，图就变成非树形图，如下：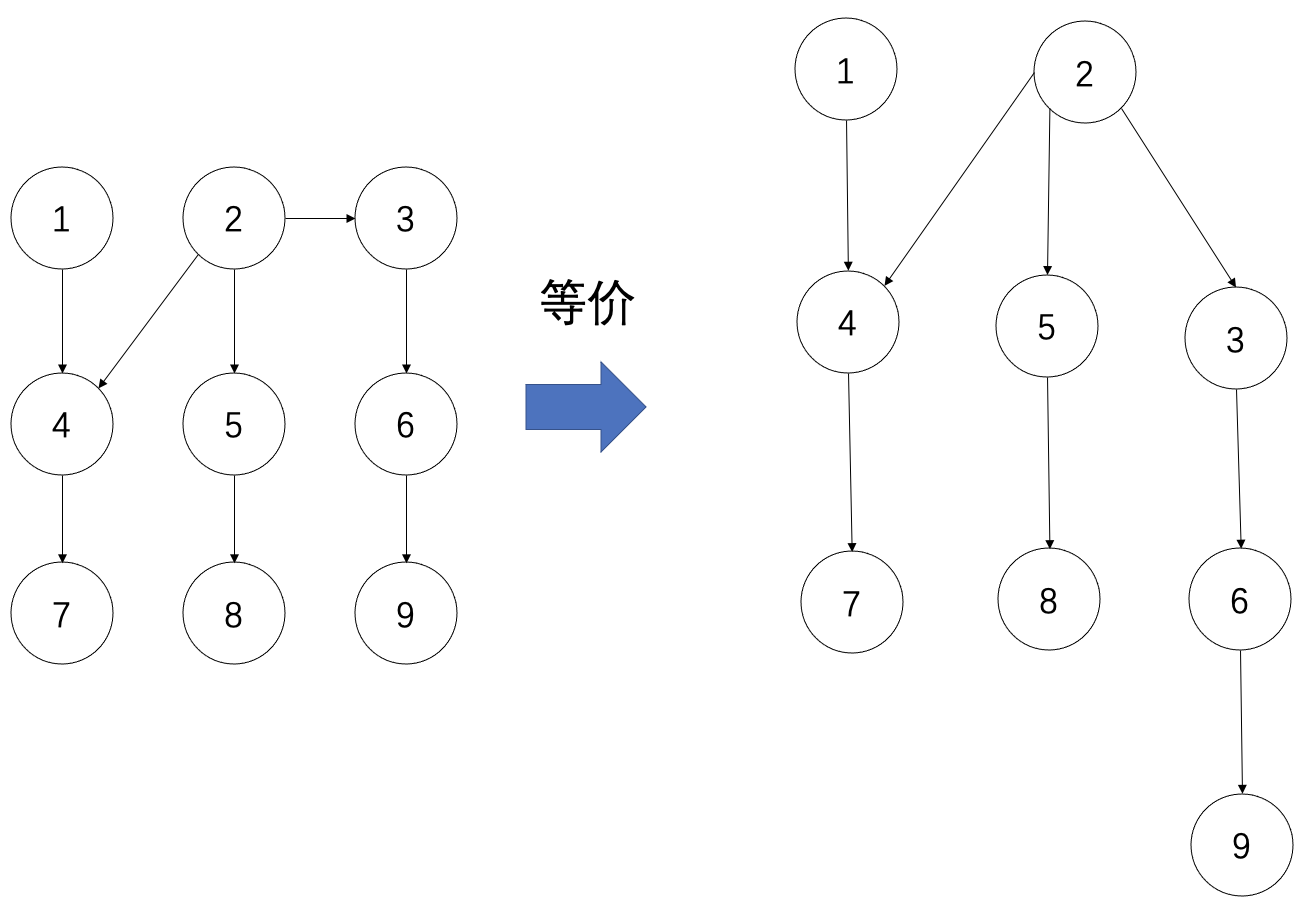

这样又回到之前多个子图的问题，我们是没法确认1号赛车和2号赛车谁快的，也就没法真正确认前两名是哪两辆赛车。

OK，至少5场比赛，而非4场比赛保证找出最快的2辆赛车得证。是不是挺难的，至少我是没有想出来，通过图论+反证法证明这个数据结论，由衷发出感慨，活学活用好难啊，能做到的大佬，真的太强了。