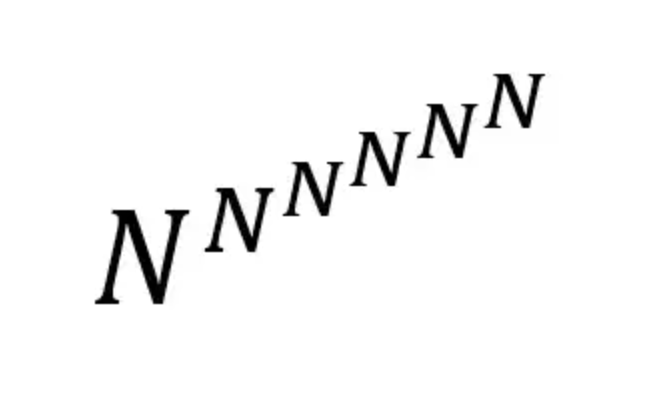导语
作者:李永乐老师官方 如何公平的切蛋糕
什么是公平?
在生活中我们会遇到各种纷争,小时候和兄弟姐妹争抢一份蛋糕,长大了到单位和同事互相举报。世界上的许多纷争,都来源于“不公平”和“嫉妒心”。
“不公平”就是感觉自己应得的没有得到,“嫉妒心”就是虽然自己得到了应得的,但是其他人得到的更多。如果设计一种方案,让每一个人都感觉自己拿到了最多的利益,纷争就会少很多。就好像把一个蛋糕分给几个人,如何才能让所有人都满意呢?
最近我看了一本书《如何切蛋糕以及其他数学问题》,颇受启发。许多管理者也许可以借鉴这个方法,一些社会矛盾也可以因此化解。下面,就让我带着大家了解一下“切蛋糕问题”吧!

一. 两人分蛋糕:我切你选
两个小孩分一块蛋糕,如果父母帮着切,经常会有孩子大喊:他的那一块比我的大。甚至有的时候,两个孩子都这样喊。
这时我们可以这样做:让一个孩子决定如何把这块蛋糕切成两份,让另一个孩子先选。切蛋糕的孩子为了不吃亏会尽量把蛋糕分得均匀,选蛋糕的孩子具有优先权,谁也不会觉得吃亏了。这就是经典的“我切你选”方式。
让我们举一个更生活化的例子:一位老人去世了,留下了一套房产和一百万现金,老人有两个儿子,但并没有留下遗嘱。于是,兄弟俩决定对房子进行评估,然后把包括房产和现金的总遗产平分。

不过,在评估房产价格时,兄弟俩产生了不同的意见——想要房子的哥哥把房产价格评估得很低,这样他除了拿到房子,还可以获得一大笔钱;不想要房子的弟弟把房产价格评估得很高,如果哥哥要房子,还要补偿弟弟一笔钱。这可怎么办?
其实这个问题不难解决,采用经典的“我切你选”的方式就可以了。首先,哥哥将房产价格进行评估,然后将总财产分成两份。一份包含房产和一部分现金,另一部分完全是现金。然后,让弟弟先选继承哪一份,剩下的一份留给哥哥。
对于哥哥来讲,他知道自己是后选择的,为了防止吃亏,他必须将遗产分配得尽量公平。如果一边明显占优,弟弟完全可以选择这一份更优厚的遗产,让哥哥吃亏。
假如哥哥刚好要结婚买房,他去市场上看了一圈,发现买相同的房子大约需要50万元,于是他就会把房子和25万现金作为一份遗产,把另外75万现金作为另外一份遗产,这两份遗产对哥哥来讲,效用都是1/2。无论弟弟如何选择,哥哥都不会感到吃亏。
对于弟弟来说,也许他在国外读大学,以后也不准备回老家工作了,所以这个房子的作用不大,他更需要钱维持自己在国外的学业。于是他评估:老人的房子只值25万,这样,第一份遗产对弟弟来讲就值50万,第二份遗产有75万,效用分别是2/5和3/5,显然,弟弟会选择第二份遗产,把第一份遗产留给哥哥。
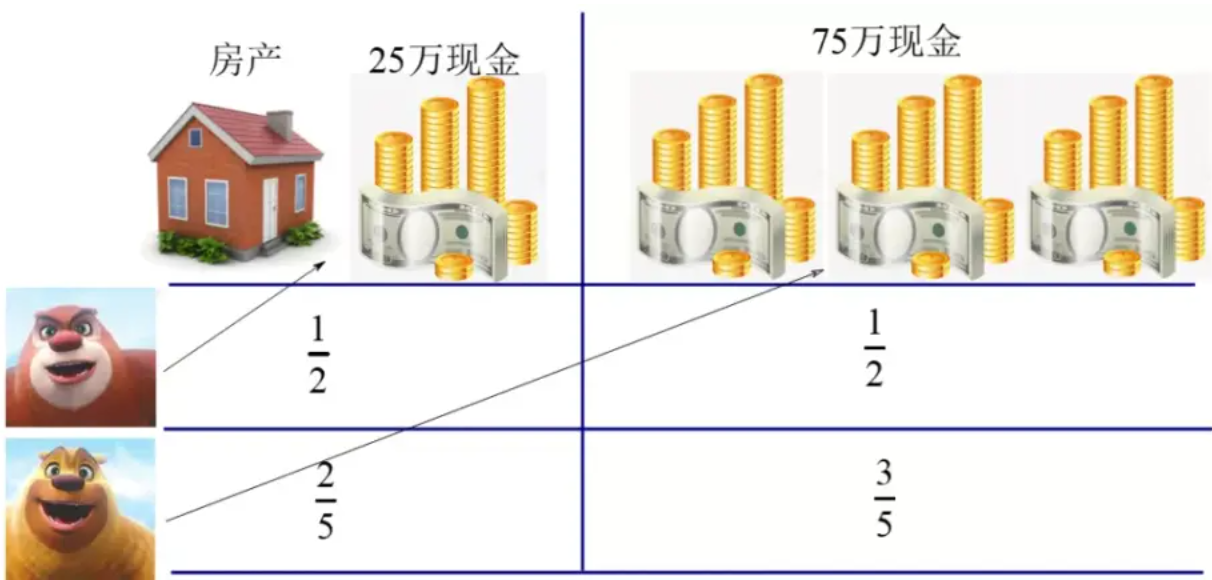
兄弟二人都觉得自己拿到了至少1/2的遗产,这就是“公平”,而且,别人拿到的都不比自己更多,这就是“无嫉妒”。由于两人对房产价值的看法不同,弟弟还觉得自己比哥哥多拿了不少,非但不会有纷争,反而因为内心惭愧而让兄弟关系变得更加和睦。
这种“我切你选”的方法,从几千年前就已经有人采用了。比如《圣经》中有这样的记载:亚伯拉罕与洛特分配迦南之地,为了公平,亚伯拉罕把这块地分为东西两块,并让洛特先选。

另一个应用是在《联合国海洋法公约》里。发达国家具有对公海矿藏进行开采的能力,但是公海矿藏应该属于全人类。于是,联合国设计了这样一种方案:如果有国家申请对公海区域进行矿产开发,需要提交两个类似区域的评估报告,联合国将在两个区域中选择一个,保留给发展中国家,另一个允许发达国家进行开采。为了自身利益,发达国家必须公正地分割区域,并如实提交报告——否则,联合国可能选择那个矿产资源更丰富的海域保留给发展中国家。

一个好的制度,不光能让人说实话,还能让所有人都觉得自己占了便宜。现在,你应该了解如何让两个人分配利益了。
二. 三人切蛋糕:公平但是有嫉妒
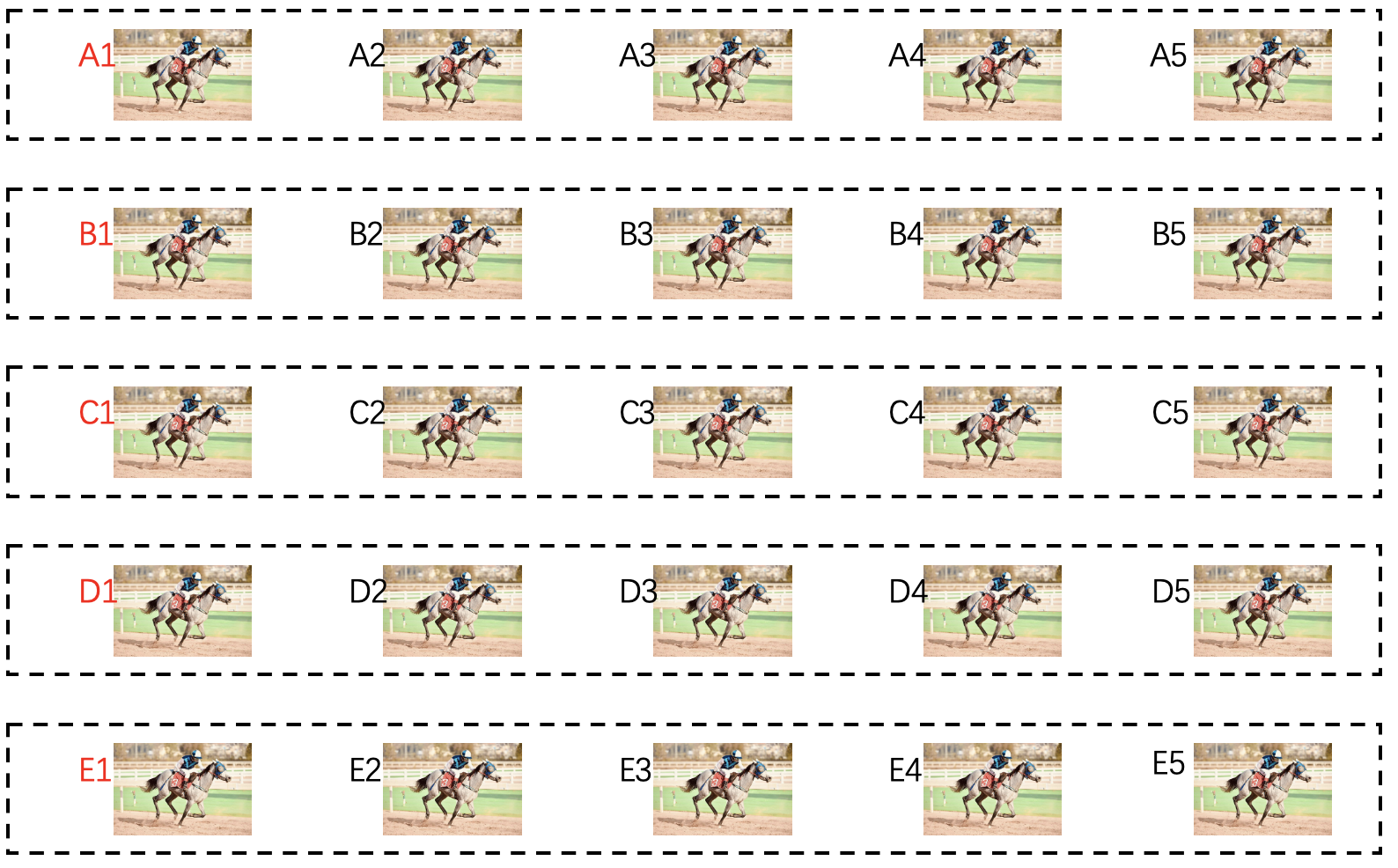
现在我们把问题升级:假如三个人要分一块蛋糕,又该怎么做呢?1961年,数学家杜宾斯和斯巴尼尔提出了一种“移动刀法”,可以让三人“公平的”分蛋糕。

假如蛋糕是一个长条,左侧有更多的草莓,而右侧有更多的奶油。现在让一个人拿着刀,缓慢地从左向右移动,三个等着分蛋糕的小朋友A、B和C紧紧盯着刀的位置,计算着自己最喜欢的蛋糕部分。
突然,小朋友A喊“停”!于是刀就在这里切下一块,并把这一块分给喊停的小朋友。随后,刀口继续移动,小朋友B又喊了一声“停”,刀又会在这儿切下一块给B,余下的一块就是C拿到的蛋糕了。
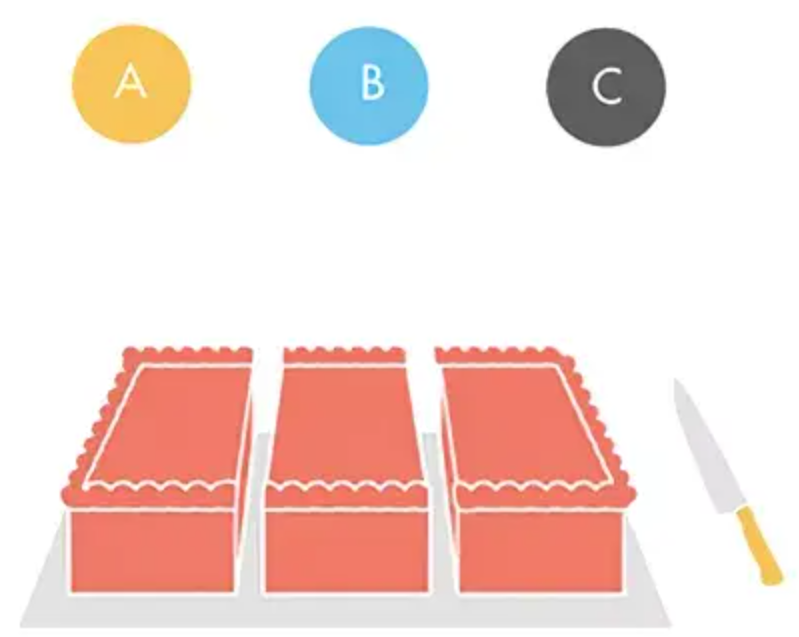
让我们来分析一下三个人的内心活动:每个人都希望自己拿到不少于1/3的蛋糕,这才是公平的。
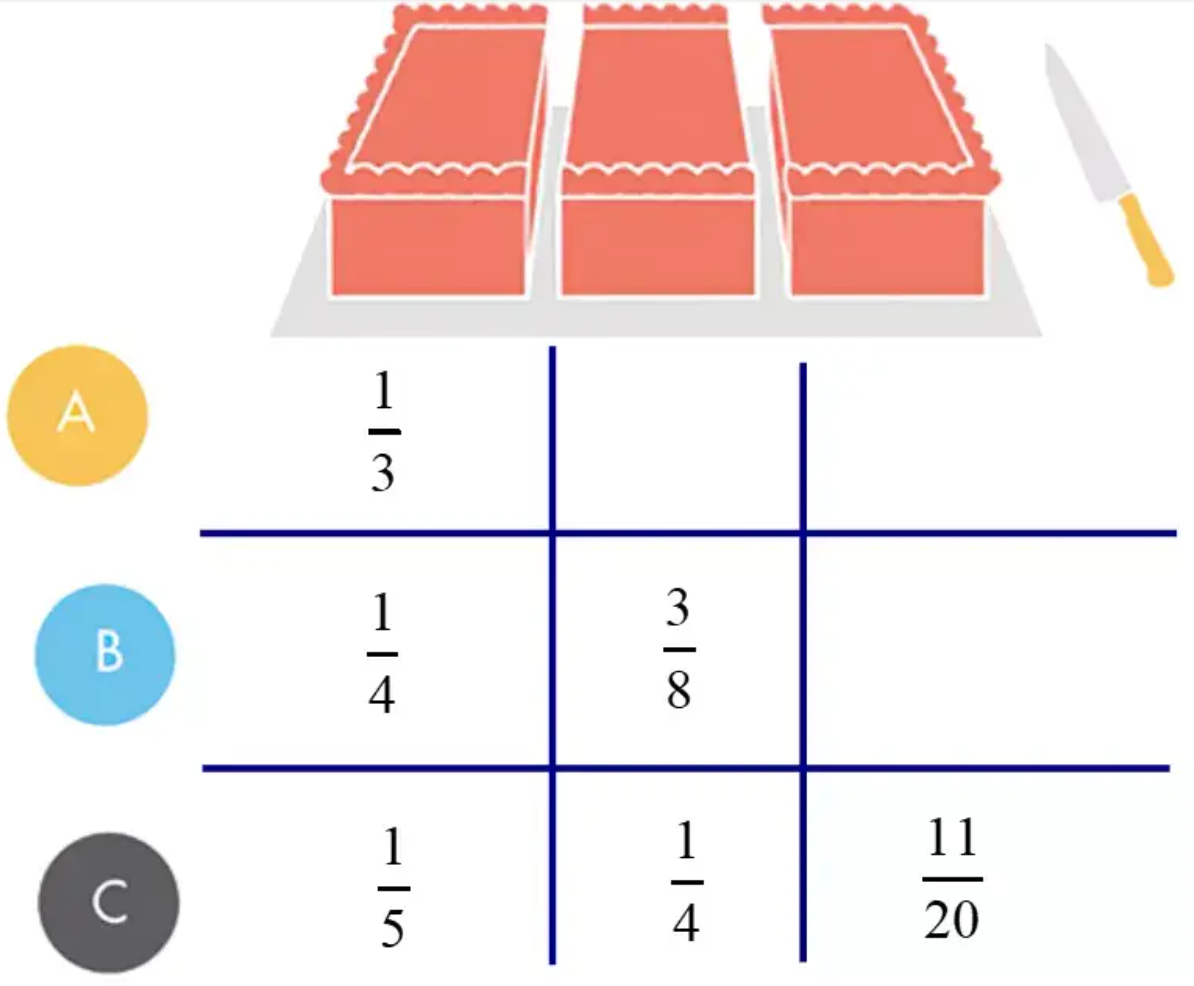
A可能特别喜欢草莓,而草莓位于蛋糕的左边。当刀移动时,A看到自己喜欢的部分被包含进来,内心激动万分,当他认为这一部分的蛋糕效用已经超过了1/3时,就会迫不及待地喊停,他已经不吃亏了。
B对草莓和奶油具有同样的喜好,当A喊停时,在B的眼中,这一块蛋糕只1/4的效用,所以B会选择继续等待。A拿走第一块后,B认为余下的蛋糕还有3/4,只剩下2个人,每人一半,自己可以拿到3/8。当刀口移动到余下的蛋糕一半的位置时,B就会喊停,拿走这一部分。
C特别讨厌草莓,又特别喜欢奶油,所以他认为A拿走的蛋糕只有1/5的效用,B拿走的蛋糕只有1/4的效用,余下的部分有11/20,结果全都被自己拿走了,C是最高兴的。
有人会有疑问:为什么A在刀口到达1/3效用的位置时一定要喊停呢?假如他再等一会儿,不就能拿到更多的蛋糕了吗?
他这样做是有风险的,因为在这个时刻,对A来讲,左侧蛋糕价值1/3,右侧蛋糕价值2/3。A喊停,可以保证拿走1/3的蛋糕;如果A选择等待,右侧部分将会少于2/3,假如此时被B喊了停,A将只能和C一起分配不到2/3的蛋糕,很有可能,A将没有机会获得1/3的蛋糕了。因此,A一定会诚实地说出自己的感受,这样他才能获得确定的、公平的蛋糕,对于B来讲,情况也是类似。
可是如果我们继续分析,就会发现这种方法尽管“公平”,却不是“无嫉妒”的。设想:在蛋糕分配完毕后,三个人重新检视了别人拿到的部分。
- C感觉A拿到1/5,B拿到1/4,自己拿到11/20,自己拿到的最多,非常开心;
- B感觉A拿到1/4,自己拿到3/8,C拿到3/8,自己和C拿到的并列最多,心情也不错。
- A看了看B和C拿到的部分,假如他觉得B拿到的部分实在糟透了,价值只有1/4,但是C因为一直没有喊停,反而拿到了最大的一块,价值是5/12(=1-1/3-1/4),比自己的1/3(=4/12)还要大!

这时,A的内心就不平静了。虽然我拿到了全部蛋糕的1/3,我并没有吃亏,但是居然有人比我拿得多,这就不行!于是嫉妒心就产生了。
这样的情景在生活中并不少见。一伙儿匪徒去抢劫,大赚了一笔,每个人都到分了不少钱,远远超过了自己的预期。可是,还是有匪徒认为别人拿到的超过了自己,于是产生了内讧。有些领导干部,明明自己贪污,反而去纪委举报同事,因为他觉得别人比自己贪污得更多,自己很冤枉。
也许你在单位中是一名兢兢业业的技术工人,有一天获得了一点荣誉或者奖金,立刻就有人红着眼睛在背后议论你,你感觉到很委屈,自己明明只拿到了应得的部分啊!为什么还会被人嫉恨呢?还是那句话,因为每个人对利益的看法不同。你认为你只拿到了自己应得的部分,但是其他人却可能觉得你比他拿的多得多。现在,你明白了吗?
三. 如何消灭嫉妒心?
三个人还有更好的分蛋糕方法吗?既要公平,还要没有嫉妒,让每个人都觉得自己拿到的部分最大?
这并不是一个容易的数学问题。在1960年代,数学家塞尔福里奇和康威提出了一个方案——三人公平无嫉妒的分蛋糕方法。

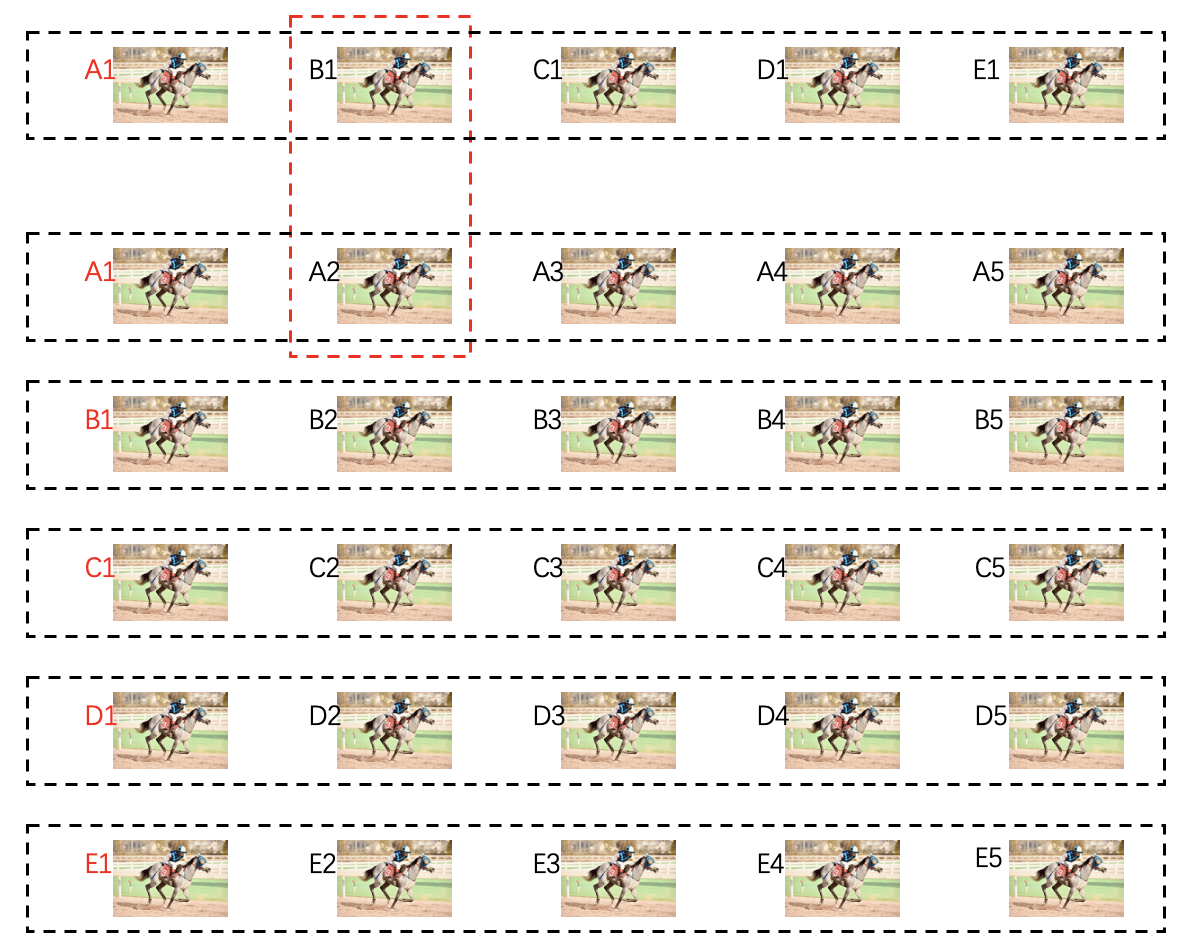
首先,让A将蛋糕分成三份,并且让B和C先选,A拿余下的那一块。因为A知道自己将会最后选择,所以他一定会尽力将三块蛋糕分成均等效用的三份,否则吃亏的一定是自己。
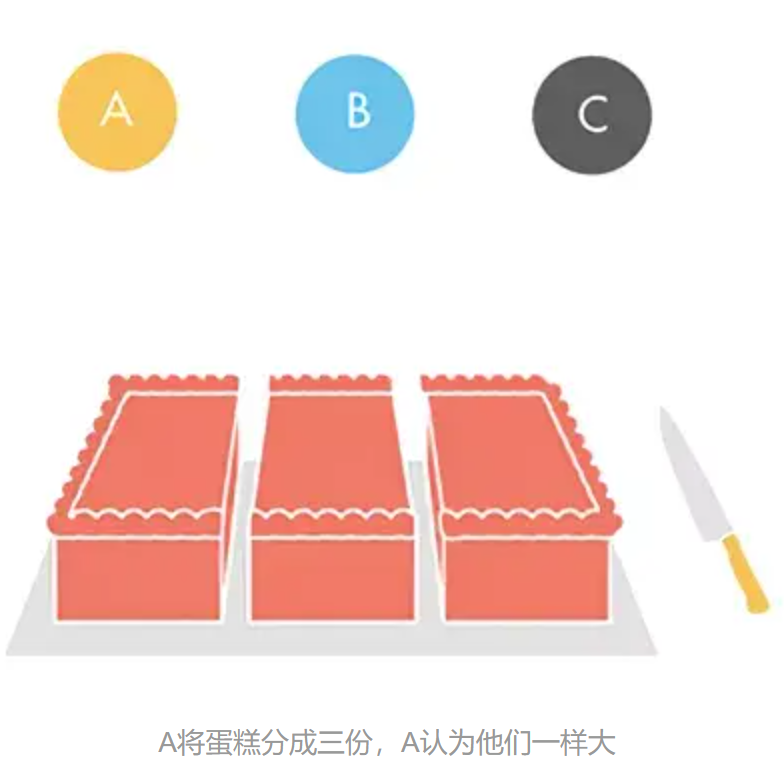
由于每个人的喜好不同,在B和C眼中,三块蛋糕并不是均等的,而是有大有小,他们都会选择自己认为最大的那一块。如果B和C的选择不同,A拿余下的一块,那么问题就解决了。此时B和C都认为自己占了最大的便宜,而A认为三块一样大,也没有人超过自己。三个人都非常开心,这种分配方案是公平且无嫉妒的。
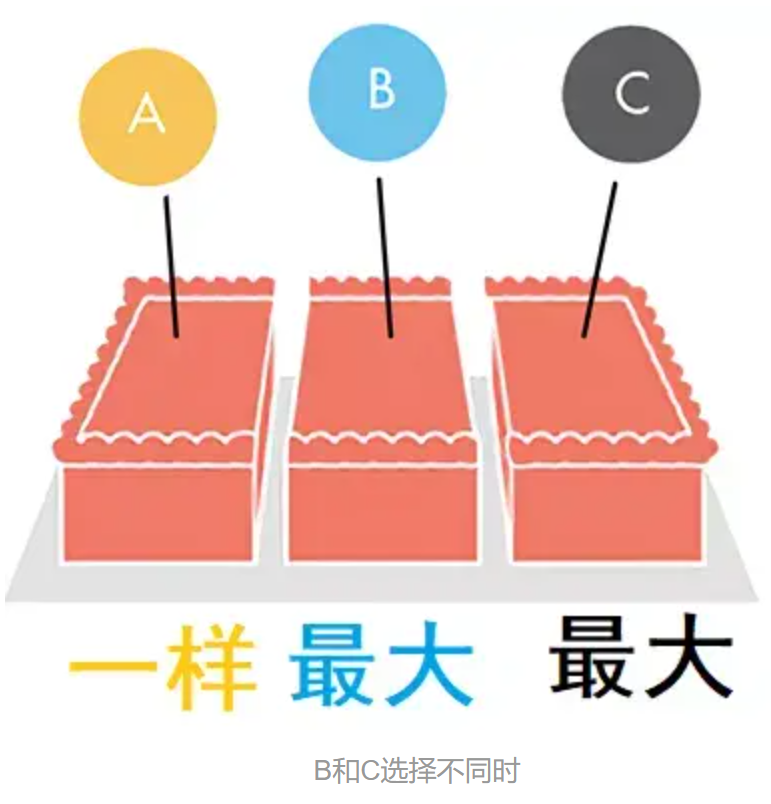
不过,如果B和C都看上了同一块蛋糕,那问题就复杂了。比如,B和C都认为右边的一块蛋糕最大,他们就必须遵循下面的步骤分蛋糕:
- 由B操刀,将最大的一块(右侧蛋糕块)再切下来一小条,使得这块蛋糕余下的部分与B眼中第二大的蛋糕块一样大。
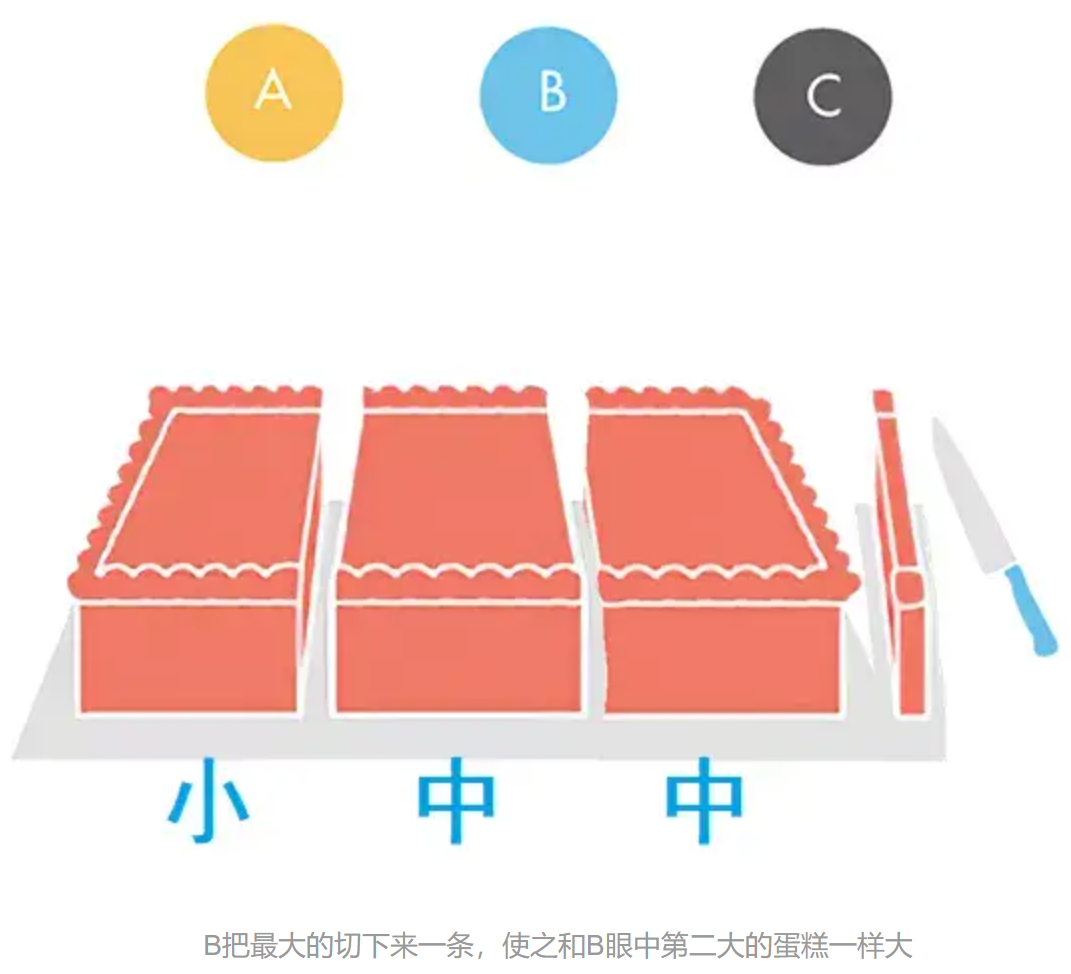
- 不考虑切下来的小条,按照C、B、A的顺序选择三个大块的蛋糕。
- 如果C没有选择B切过的那一大块蛋糕(右侧蛋糕),那么B必须自己拿走这一块。
这个过程类似于新闻上4S店的新车争夺战。一名男顾客和一名女顾客同时看中了一台新车争执不下,此时男顾客飞起一脚把新车的车灯踹碎了,并问女顾客:这辆车你还要不要?你要的话我还继续踹。此时,如果女顾客选择退出,男顾客就必须自己把这辆车买走,否则4S店是不会同意的。
按照这个步骤,三人在第一次分配的过程中,都感觉自己是占便宜的。
- C先选,C一定选择自己心目中最好的一块,他没有理由嫉妒别人;
- B再选,因为经过自己操刀,三块蛋糕中有两个蛋糕相同而且最大(比如中间的和右侧的),C不可能把两块都拿走,所以B总有机会拿走最大的两块中的一个;
- A最后选,原本他将蛋糕切成了三个一样大的,现在由于B将最右侧的蛋糕又切下来一块,最右侧的蛋糕变小了,左侧和中间的蛋糕一样大。不过好在,如果C没有把最右侧的蛋糕拿走,按照规则B就会把这一块拿走,这块小的蛋糕一定不会留给A,A也非常开心。

大块分完了,现在开始分切下来的一小条。如果刚才,C拿走了最右侧的一块(那个被B切过的)蛋糕,那么就继续由B将这一小条分成均匀的三块,并且按照C、A、B的顺序选择这三块,这样同样是无嫉妒的。

- C第一个选,所以他会选择自己心目中最好的那块,不会嫉妒别人。
- A比B先选,所以A不会嫉妒B;又因为在A心中,现在分的这一小条,本来就是从刚刚被C选走的那一块(最右侧)的蛋糕上分割下来的,在A的眼中,C这个傻子上一次选了最小的,现在就算把这三个部分全都给C,C也只是拿到跟自己一样多的蛋糕而已。于是,A也不会嫉妒C。
- B最后选,他一定会尽力将三块分得均匀——无论自己拿到哪一块,都不会嫉妒别人。
这样,整个蛋糕被分配完毕。三个人都觉得自己拿到了最大的一块,这样就不会有人嫉妒别人,也不会有人到上级部门举报了。这真是一个精妙绝伦的方法!

如果刚才是B选择了被切过的蛋糕块(最右侧),那么就由C来分配这小块,再按照B、A、C的顺序选择,结论和刚才一样。
如果人数比三个人还多,又该怎么做才能公平且无嫉妒的分蛋糕呢?1995年,数学家布拉姆斯和泰勒证明了无论有多少人,都存在这样的分配蛋糕方案。只是,在人数比较多的时候,这个分配方法非常的复杂。

到了2016年,阿奇兹和麦肯奇又证明了N个人公平且无嫉妒的分配一个蛋糕,所需要的方法数的上界是:
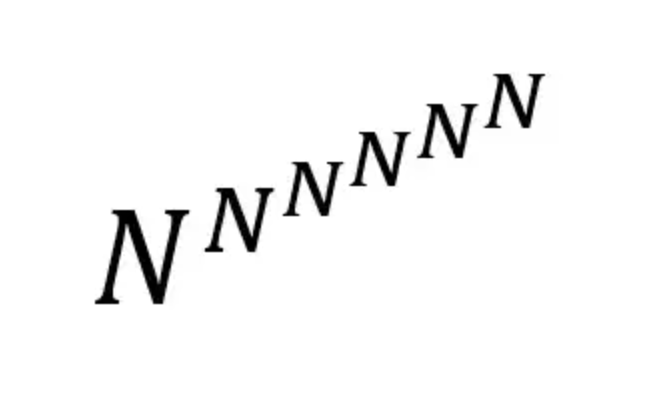
这么多种。
尽管这个问题在数学上的解非常复杂,但是它依然能给我们看待社会问题很多的启发。比如作为公司员工,我们会明白自己为何会嫉妒别人,以及为何会被别人嫉妒;作为公司管理者,我们自认为是客观公正的,但是员工却都觉得自己偏心。
家长们自认为自己是客观公正的,呕心沥血地设计方法分蛋糕,反而经常会落个里外不是人的结局。相反,设计一个合力的制度,让孩子们参与到分蛋糕的过程中,没准能获得一个让所有人都满意的结果。