俄罗斯方块:“富贵险中求”算法
导语
作为80后,小时候一定玩过一款经典游戏,俄罗斯方块,英文名称Tetris。玩的画面在脑海中已是“上古”时期的事情,但也并不陌生,因为刷视频时,偶尔还能看到顶尖世界高手对决,他们玩的俄罗斯方块难度极大,游戏模式是对决,比谁的分数高,有些比赛到最后不仅自己消砖块得分,而且还可以通过得分不停给对手制造麻烦。
看到鹅厂组织的一次极客挑战赛,主题就是俄罗斯方块游戏,当然游戏名称叫“鹅”罗斯方块,蛮鹅厂风格的,可可爱爱。

我比较感兴趣,当时也报名参加了,最后是在2000+入场选手排名在9位,比赛结束后,我又花了点时间调试了自己的算法参数,最终比赛分数可以刷进TOP3。谨以此文,记录自己的所思所想。
如何活着
第一步想到的是,如何“活着”,就和当前经济形势下,各行各业都得考虑先“活着”,能不能得到高分其次,先得“不死”。
我自己写了一个俄罗斯方块的游戏界面,和传统俄罗斯方块游戏一样,如何拼搭这些小图形,让高度不超过游戏规定的高度,满行就会消除,消除的行数有4种情况1行、2行、3行和4行。针对如何活着的俄罗斯方块AI算法比较多了,全网比较有名的是Pierre Dellacherie算法。我这里搜索到一篇El-Tetris – An Improvement on Pierre Dellacherie’s Algorithm,大家可以参考下。
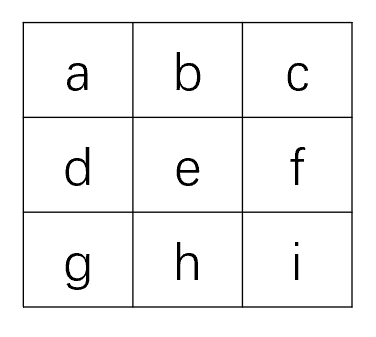
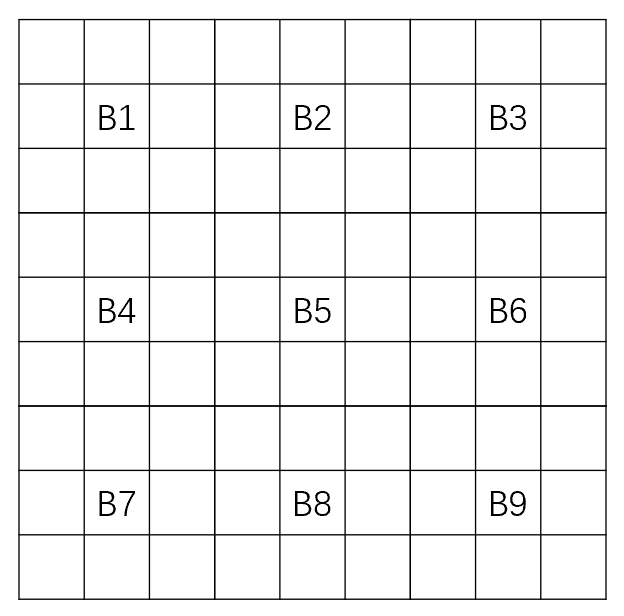
首先,分析下俄罗斯方块中方块的种类,一共有7种图形: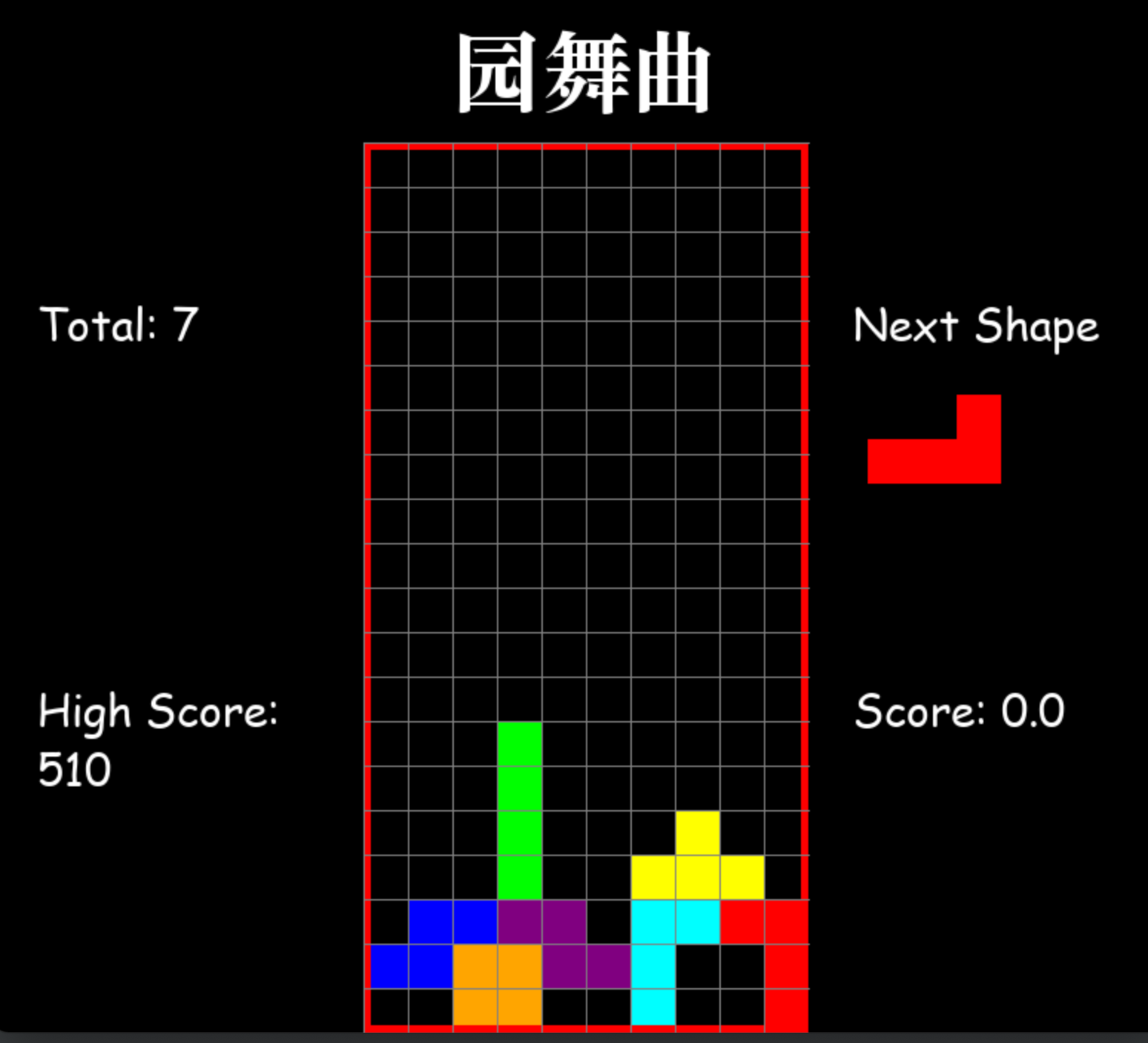
上面图中有7种不同的形状,我在代码里面的表示为坐标法,以(0, 0)为原点,标示周围那几个点对应图形需要占用。
BrickShapes = [
# I
[[[-2, 0], [-1, 0], [0, 0], [1, 0]],
[[0, -1], [0, 0], [0, 1], [0, 2]]],
# L
[[[-2, 0], [-1, 0], [0, 0], [0, 1]],
[[0, 0], [0, 1], [0, 2], [1, 0]],
[[0, -1], [0, 0], [1, 0], [2, 0]],
[[-1, 0], [0, -2], [0, -1], [0, 0]]],
# J
[[[-2, 0], [-1, 0], [0, -1], [0, 0]],
[[-1, 0], [0, 0], [0, 1], [0, 2]],
[[0, 0], [0, 1], [1, 0], [2, 0]],
[[0, -2], [0, -1], [0, 0], [1, 0]]],
# T
[[[0, -1], [0, 0], [0, 1], [1, 0]],
[[-1, 0], [0, -1], [0, 0], [1, 0]],
[[-1, 0], [0, -1], [0, 0], [0, 1]],
[[-1, 0], [0, 0], [0, 1], [1, 0]]],
# O
[[[-1, 0], [-1, 1], [0, 0], [0, 1]]],
# S
[[[-1, 0], [-1, 1], [0, -1], [0, 0]],
[[-1, -1], [0, -1], [0, 0], [1, 0]]],
# Z
[[[-1, -1], [-1, 0], [0, 0], [0, 1]],
[[-1, 0], [0, -1], [0, 0], [1, -1]]]
]比如竖棍“I”的图形,有两种rotation,所以有两组坐标的标示方式,其他图形类似,只不过rotation数量不同:
# I, two rotations
[[[-2, 0], [-1, 0], [0, 0], [1, 0]],
[[0, -1], [0, 0], [0, 1], [0, 2]]],
El-Tetris算法是传统AI人工智能,不要因为人工智能,就觉得很复杂,其实不论传统的AI算法还是目前深度学习的人工算法,一般都不会很复杂,深度学习AI算法不在此文讨论范围。基本上传统AI算法就是列举所有的可能性,通过计算预先建模的公式,评估最优秀的一个局面,做出选择,一直循环往复,直到游戏结束。我们看下El-Tetris算法的公式:
f(x) = b0x0+b1x1+b2x2...bnxn
其中x0,x1,x2...xn都是一些特征,b0,b1,b2...bn是一些系数(通过数学方法或者机器学习方法等手段推算出的经验值),对应特征和系数相乘相加之后,得到的就是当前局面+此选择的局面评估分数,是不是很简单,看上去是一个线性公式,但是效果出奇的好,原因还是在于每一个特征x的合理性以及系数b的合理性。
系数b不需要我们实现,就是一组常数字,作者说是通过particle swarm optimization寻找到的,具体怎么找,我也不太清楚,先拿来用吧。
另外要提一下,算法可以通常可以考虑当前图形+下一个图形,也可以只考虑当前图形,据说效果差不多,我这里只考虑当前图形的所有可能的操作,每一个图形出来,其实只需要考虑图形放置的position和rotation两个变量。所以整体的流程:
while the game is not over:
examine piece given
find the best move possible (an rotation and a position)
play piece
repeat
上面铺垫这么多,那么一共建模了几种特征呢?一共是6种,如下:
- Landing Height: The height where the piece is put (= the height of the column + (the height of the piece / 2)).
- Rows eliminated: The number of rows eliminated.
- Row Transitions: The total number of row transitions. A row transition occurs when an empty cell is adjacent to a filled cell on the same row and vice versa.
- Column Transitions: The total number of column transitions. A column transition occurs when an empty cell is adjacent to a filled cell on the same column and vice versa.
- Number of Holes: A hole is an empty cell that has at least one filled cell above it in the same column.
- Well Sums: A well is a succession of empty cells such that their left cells and right cells are both filled.
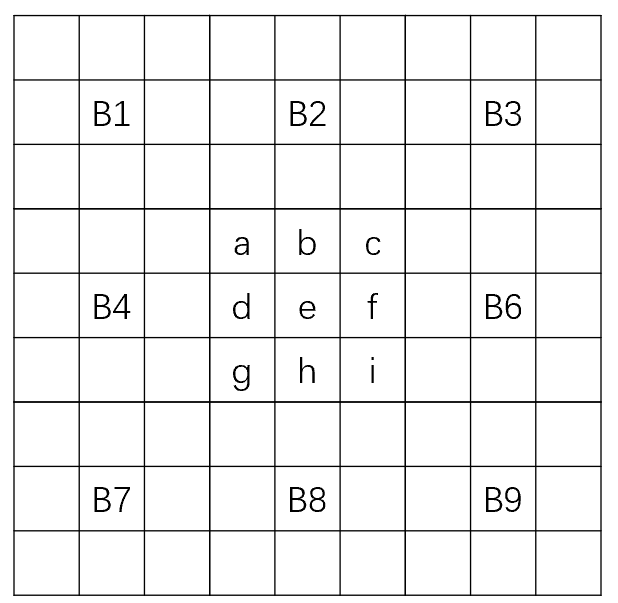
Landing Height和Rows eliminated比较好理解,其他对着下图解释下: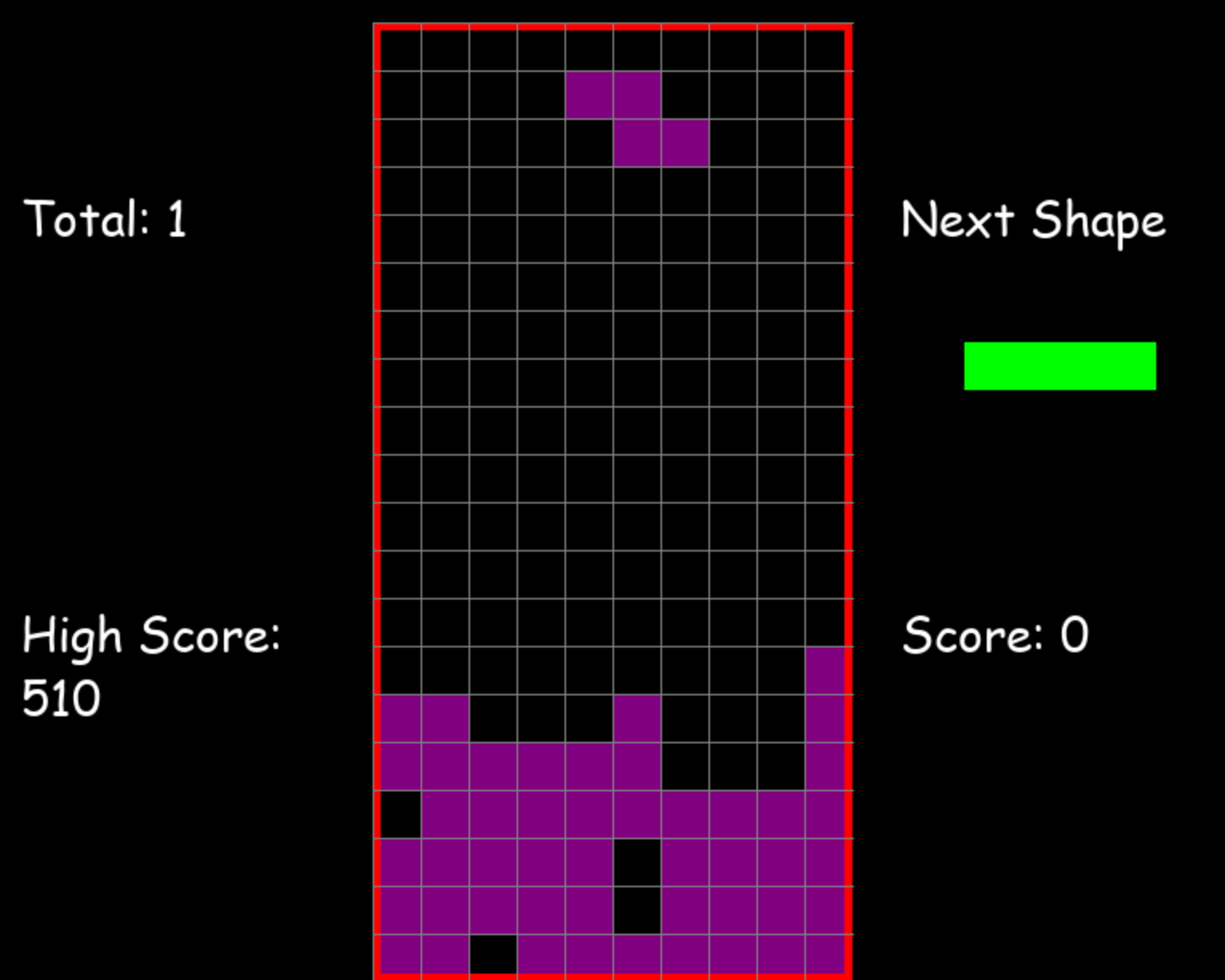
Row Transitions总数是16,最底部一行为2,依次往上2、2、2、2、4、2,注意我这里处理为左右边界外是被占据的,所以倒数第四行靠最左边有个空,算存在一次row transition,另外空行我没算(我猜测也可以计算row transition,不影响最后结果)。
Column Transitions总数是26,如果理解了Row Transitions,这个计算方法是一样的。
Number of Holes总数是4,看下上图,应该知道什么叫“洞”,被封闭了的空单元格。
Well Sums总数是5,如果左右两边单元格被占,顶上又没有被封闭,可以算作一个“井”格子,第一列一个单元格,左边界外算占据,右边也被占据,所以也算作“井”格子,深度为1,第三列就一个单元格,井深度为1,第六列有2个空单元格,井深度和为1+1+1+2。这个比较难理解,多看几遍。
对应的系数如下:
Landing Height = -4.500158825082766
Rows eliminated = 3.4181268101392694
Row Transitions = -3.2178882868487753
Column Transitions = -9.348695305445199
Number of Holes = -7.899265427351652
Well Sums = -3.3855972247263626
计算代码如下:
def find_best_play(current_piece, grid):
if current_piece.y < 0:
False, 0, 0
rotations = len(current_piece.shape)
x_moves = [-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5]
rotation = 0
x_move = 0
best_play_score = float("-inf")
for i in range(rotations):
for j in x_moves:
candidate_piece = copy.deepcopy(current_piece)
candidate_grid = copy.deepcopy(grid)
candidate_piece.rotation += i
candidate_piece.x += j
if not (valid_space(candidate_piece, candidate_grid)):
continue
valid, score = evaluate(candidate_piece, candidate_grid)
if valid and score > best_play_score:
best_play_score = score
rotation = i
x_move = j
return True, rotation, x_move
def evaluate(current_piece, grid):
while True:
current_piece.y += 1
if not (valid_space(current_piece, grid)) and current_piece.y > 0:
current_piece.y -= 1
break
shape_pos = convert_shape_format(current_piece)
for i in range(len(shape_pos)):
x, y = shape_pos[i]
if y > -1:
grid[y][x] = current_piece.color
heights_points = (20 - current_piece.y + current_piece.height[current_piece.rotation % len(current_piece.height)]) * float(-4.500158825082766)
rows_removed = get_rows_removed(grid) * float(6.4181268101392694)
rows_transitions = get_row_transitions(grid) * float(-3.2178882868487753)
cols_transitions = get_col_transitions(grid) * float(-9.348695305445199)
num_of_holes = get_num_of_holes(grid) * float(-14.899265427351652)
wells = get_well_sums(grid) * float(-6.3855972247263626)
return True, heights_points + rows_removed + rows_transitions + cols_transitions + num_of_holes + wells
find_best_play列举所有可能的操作,evaluate就是评估局面的分数,其中几个计算特征值的函数:
def get_row_transitions(grid):
rows = len(grid)
cols = len(grid[0])
transitions = 0
last_pos = True
for i in range(rows - 1, -1, -1):
if is_empty_row(grid[i]):
continue
for j in range(cols):
if (grid[i][j] in brick.SHAPES_COLORS) != last_pos:
transitions += 1
last_pos = (grid[i][j] in brick.SHAPES_COLORS)
if not last_pos:
transitions += 1
last_pos = True
return transitions
def get_col_transitions(grid):
rows = len(grid)
cols = len(grid[0])
transitions = 0
last_pos = True
for j in range(cols):
for i in range(rows - 1, -1, -1):
if (grid[i][j] in brick.SHAPES_COLORS) != last_pos:
transitions += 1
last_pos = (grid[i][j] in brick.SHAPES_COLORS)
if not last_pos:
transitions += 1
last_pos = True
return transitions
def get_num_of_holes(grid):
rows = len(grid)
cols = len(grid[0])
holes = 0
previous_row_holes = [0 for _ in range(cols)]
for i in range(rows)[1:]:
for j in range(cols):
if grid[i][j] == (0, 0, 0) and (grid[i-1][j] != (0, 0, 0) or previous_row_holes[j] == 1):
holes += 1
previous_row_holes[j] = 1
return holes
def get_well_sums(grid):
rows = len(grid)
cols = len(grid[0])
well_sums = 0
# Check for well cells in the "inner columns" of the board.
# "Inner columns" are the columns that aren't touching the edge of the board.
for j in range(cols-1)[1:]:
for i in range(rows - 1, -1, -1):
if grid[i][j] == (0, 0, 0) and grid[i][j-1] != (0, 0, 0) and grid[i][j+1] != (0, 0, 0):
well_sums += 1
k = i+1
while k < rows:
if grid[k][j] == (0, 0, 0):
well_sums += 1
else:
break
k += 1
# Check for well cells in the leftmost column of the board.
for i in range(rows - 1, -1, -1):
if grid[i][0] == (0, 0, 0) and grid[i][8] != (0, 0, 0):
well_sums += 1
k = i + 1
while k < rows:
if grid[k][0] == (0, 0, 0):
well_sums += 1
else:
break
k += 1
# Check for well cells in the rightmost column of the board.
for i in range(rows - 1, -1, -1):
if grid[i][cols-1] == (0, 0, 0) and grid[i][cols-2] != (0, 0, 0):
well_sums += 1
k = i + 1
while k < rows:
if grid[k][cols-1] == (0, 0, 0):
well_sums += 1
else:
break
k += 1
return well_sums
完成后的效果特别好,尽管一度高度和累积的形状不太好看:
但是AI会慢慢控制住局面,变成如下局面:
我尝试自己手动玩了下,鹅厂给出的图形顺序,还真的不是很好玩,稍不小心就挂了,因为图形的占比不是均分的,S型和Z型比较多,过了一会,貌似EI-Teris算法也会“顶”不住。。。
仔细看了下方块图形生成的代码,每个方块图形的生成概率不等,比如长条“I”型的生成概率才2/29:
def getShapeIndex(self):
weight = self.rand_number % 29
shape_index = 0
if 0 <= weight <= 1:
shape_index = 0
elif 1 < weight <= 4:
shape_index = 1
elif 4 < weight <= 7:
shape_index = 2
elif 7 < weight <= 11:
shape_index = 3
elif 11 < weight <= 16:
shape_index = 4
elif 16 < weight <= 22:
shape_index = 5
else:
shape_index = 6
return shape_index
所以正常的俄罗斯方块AI算法远远不够,调整了一下估值函数的系数(针对掉落方块形状分布不均的情况),我发现最多也只能获得20w分不到(方块图形数量仅仅10000块),离当天的第一名130w+分,差距很大。
追求“财富”
仔细理解下鹅罗斯方块的积分规则,“富贵险中求”:
由于就仅仅有10000块方块,我考虑使用动态规划,将所有可能的局面求出,再计算能够累积得到的最大分数,当然,由于状态总数有2^200之多,保存所有的局面不现实,必须要舍去大部分的局面。一开始的想法是:在扩展的过程中,按照安全性估价函数筛查出固定数目状态进行保存(目标是局面安全),经过固定步数,再对分数进行贪心,取出唯一最高分状态继续扩展(目标是高分),这样反反复复尝试,不行,因为太早贪心,容易丢失掉“潜力”的局面,后面会得到高分局面,所以尽可能保留安全局面,所谓“留得青山在,不怕没柴烧”,直接把分数的因素引入估价函数,不再额外对做分数做贪心。
evaluation = board_evaluator.Evaluate(k) - v.score * self.score_weight
其中board_evaluator.Evaluate(k)中,k就是当前局面,self.score_weight我手动尝试出来的取值为1/38,Evaluate函数就是:
PARAMS = [
-1,
3.2178882868487753,
9.348695305445199,
7.899265427351652
# 3.3855972247263626
]
def Evaluate(board):
return PARAMS[0] * board.getCount() + PARAMS[1] * board.getRowTransition() + \
PARAMS[2] * board.getColTransition() + PARAMS[3] * board.getNumberOfHoles()
其中Landing Height和Well sums两个特征不再评估函数内,甚至我觉得“井”的局面对取得高分是有益的(没尝试加回来,可以试试看),另外增加了当前局面下的被占据了的格子总数和当前可以得到的分数和。靠着这个估值函数,对于当前方块放置完成的局面只保留100个最好的(评估分数最高的),一直迭代到10000个,取出得分最高的局面,还原出所有的操作列表,在本地模拟AI的操作,效果特别棒,AI会自动的留一条缝,尝试将其他空间填满填好,比赛期间取得了85w的分数,赛后我手动调试后,分数涨到125w左右,效果图如下所示:
总结
总结的文章看上去很简单,其实过程特别煎熬,反反复复在本地尝试,实现过程也有不少小问题,调试起来也很麻烦,有怀疑、有纠结、有确定,到最后的效果符合预期,真的不容易,比如为啥score_weight要取1/38,估值函数的整体建模,为什么要减除这个特征,要加另外一个特征,怎么剪枝。整个比赛期间,我只取得了85w的分数,赛后再经过调试得到了125w的分数,就叫此算法为“富贵险中求”算法,可以使用此算法的前提是必须知道方块完整的掉落顺序。