最近参加了一场极客挑战赛，挺有意思的，准备简单写下笔记。整个比赛是以游戏形式让大家参与的，一共四个，一开始的时候，我以为真的可以靠纯手打，去进行通关，后来发现，想得太天真了。四个游戏，都是需要通过一些编程去解决的，我过了大部分关卡，不过有些是靠的运气，看完官方的题解后，又有了新的认知。

第一个游戏是类似回合制RPG游戏，类似：

画面没这么好哈，版权原因不能用游戏原图，总之有一个行动条，到了时间就可以行动，英雄（就1个）和怪物（一场战斗也就1个）互相攻击，主角在一个地下城堡，总共24层，一层一层往下冲关，每层会有一个宝箱，每次进入下一层，地图都是随机选择的，地图模式有简单、困难和BOSS，每经过8层，地图中怪兽会升级。

英雄是有技能池的，选择什么技能攻击怪兽，是可以进行策略选择的。
英雄的数据：

hero = {
    "Attack": 30,
    "Hp": 200,
    "Mp": 200,
    "Skills": {
        "skill_0": {
            "Cost_mp": 0,
            "Power": 1
        },
        "skill_1": {
            "Cost_mp": 10,
            "Power": 1.5
        },
        "skill_2": {
            "Cost_mp": 20,
            "Power": 2
        },
        "skill_3": {
            "Cost_mp": 30,
            "Power": 2.5
        }
    },
    "Speed": 30
}

典型的怪物数据：

"Monsters":[
    {
        "Attack":30,
        "Hp":40,
        "Speed":25
    },
    {
        "Attack":20,
        "Hp":50,
        "Speed":20
    }
]

上面的Monsters数据是简单地图的，字段都还比较好理解哈，不多做解释了。
游戏还有一个设定，如果是非8、16、24层，每层都有一个宝箱，这个宝箱是随机开出来奖励或者惩罚，一共有4种情况：

1. empty_box，空箱子；
2. add_hp_mp，加血又加魔法值，Hp+10且Mp+50；
3. del_hp，扣10血；
4. 升级属性，可以选择Attack+10，Speed+1，Hp+100，Mp+200；

是不是感觉这些写出来变量都有点多了，而且都是靠自己抓包，分析出来的，其实玩的时候，真的需要一点点琢磨。然后我通过手打1～8层，发现了一些规律：

• 如果英雄和怪兽Speed一样，英雄是占先的，也就是速度这块，玩家是占点便宜的；
• 通过抓包发现，整个游戏和后端交互的协议就三条吧，new_level（重开游戏），next_layer（进入下一层），和open_box（开宝箱）；

new_level请求和回包：

{token: "YOUR_TOKEN"}
{"code":0,"data":{"hero":{"Attack":30,"Hp":200,"Mp":200,"Skills":{"skill_0":{"Cost_mp":0,"Power":1},"skill_1":{"Cost_mp":10,"Power":1.5},"skill_2":{"Cost_mp":20,"Power":2},"skill_3":{"Cost_mp":30,"Power":2.5}},"Speed":30},"star_num":3},"message":""}

open_box请求和回包：

{"Layer_idx":1,"token":"YOUR_TOKEN"}
{"code":0,"data":{"box":{"BoxType":"add_hp_mp","Value":[30,50]}},"message":""}

next_layer请求和回包：

{"Layer_idx":1,"Choice":"left","Layer_ops":[["start_battle",0],["battle_op",170,200,[["Hero","skill_0"],["Monster","skill_0"],["Hero","skill_0"]]],["start_battle",1],["battle_op",150,190,[["Hero","skill_1"],["Monster","skill_0"],["Hero","skill_0"]]],["open_box"]],"token":"06xyzzou0074CFBD948B14E238FB24BC"}
{"code":0,"data":{"layer":{"Layer_idx":2,"Map_mode":"boss_map","Monsters":[{"Attack":30,"Hp":100,"Speed":40}]}},"message":""}

• 在客户端清理了一层的怪物后，可以选择去下一层的两扇门（left or right），这时候客户端会发送后端，玩家在这一层执行的所有动作序列（看上面的示例），然后后端会根据客户端上传的序列，在后台重放，看看动作序列是否合法，合法就可以进入下一层；

上面这些都是我通过手打1～8层，发现的一些规律，然后我进入第9层，发现怪物确实变强了些，那么通过上面的观察，我第一个想法是每次对怪物的击打，都要经过最优策略的选择，这个最优策略我想了下，每次打怪物的时候，我最终击败他时，保证Hp+Mp是最大的，这个算法我通过bsf，广度优先搜索，大概写了3个小时（也debug了一会），终于写出来了，其实最开始，我天真的以为每次只要固定动作序列即可，什么意思，就是我手动计算一遍简单、困难和boss的地图，会产生什么合法的对列，然后直接发几个构造好的next_layer的请求即可，后来发现，果然是天真了，极客挑战赛，不可能是这么蠢的解法（当然我觉得也是有可能能通过的，毕竟怪物属性值不是随机的，就那么几种）。但是作为程序员，怎么能都通过手动算呢，所以我就写了一个和怪物战斗时的最优策略选择算法。代码不贴了，思路是这样的：

1. 通过计算总共可能的最多攻击次数，英雄最多的攻击次数 = 怪物血量/英雄普通攻击（不耗魔的那个），怪物攻击的最多次数 = 英雄血量/怪物攻击力，选较小的次数保留下来；
2. 在最小的次数规定的时间内，把英雄和怪物可以行动的时间点插入到一个数组（理论上速度够快的一方，其实可以“套圈”，当然实际游戏数据中未出现这种数据）；
3. 把2计算得到的数组进行排序，得到一个按时间排序好的有序时间数组，数组元素记录了轮到哪一方行动，这里有一个小tip，因为上面发现了英雄和怪物速度一样的时候，英雄占先，所以偷偷给怪物行动时间加一个小的偏移量，这样排序后的结果保证了相同速度时，英雄在怪物前行动；
4. 按上述有序数组，挨个做动作，如果怪物动，就一种行动，用他的普通攻击攻击英雄，如果英雄动，英雄有4种行动可选，挨个试，合法状态继续bfs；
5. 直到怪物死掉，这个动作序列是有效的，保存下来（不仅保存动作，也保存英雄剩余的Hp和Mp）；
6. 得到所有可能的有效动作序列后（有效指的是英雄杀死了怪物），看看哪一个序列Hp+Mp最大，执行这个动作序列；

宝箱我就每层都打开，这里也有策略，因为有一个宝箱是提升英雄属性，我一开始是Hp<1.5Mp，加Hp，Mp<150加Mp，Hp和Mp都健康，加Attack，后来发现这个策略不行，第二阶段（9～16层），里面有个怪物的Speed是31，英雄默认的Speed是30，这不欺负人吗？

果断在1～8层有机会先Speed+1，然后尽可能在血量健康状态下加Attack，这样跑了4个小时，被我跑到了接近16层，但是后面还是会挂，那怎么办呢，嗯，我想到了，启动一个后台进程，一直跑，嘻嘻。。。

一值跑的过程很煎熬，因为不知道这么做是不是能打穿24层的地堡，我当时觉得组委会肯定不是这么设计题目的，后来证明这确实是暴力过题的一种方法，跑了20+小时，我查看了日志，发现一个问题，有些运气爆棚的时候，确实可以避开扣血宝箱，而且尽可能加属性，加Hp和Mp，地图也是大多数是简单的，达到过21层，在22层时，遇到一个攻击400，Speed超级快的Boss，基本没有还手之力，我突然郁闷了。。。

在内部的讨论群，我发现很多人都说自己就是暴力通过的，得靠人品，所以又等了接近一天，皇天不负有心人，真的通过啦，那一刻，我快乐得像个孩子，好开心啊～

但是故事还没结束，官方题解下来后，我发现自己漏了一个（或者不是漏了，是根本没往那方面想）点，在第七层，有一段代码会展示给选手，大概是这样的：

func ProcessOneUser(nowLayerId int, queryCMD string, choice string) string {
    r := rand.New(rand.NewSource(time.Now().UnixNano()))

    for {

        if queryCMD == "open_box" {
            if nowLayerId == 8 || nowLayerId ==16 || nowLayerId == 24 {
                return "new_star"
            } else if nowLayerId == 7 {
                return "secret_code"
            } else {
                switch r.Int63() % 4 {
                case 0:
                    return "empty_box"
                case 1:
                    return "add_hp_mp"
                case 2:
                    return "del_hp"
                case 3:
                    return "add_skill"
                }
            }
        } else if queryCMD == "next_layer" {
            newLayerId := nowLayerId + 1

            // rest_map 休息房，没有怪物
            // easy_map 简单层，有两个怪物
            // hard_map 困难层，有三个怪物
            // boss_map boss层，有一个boss
            if newLayerId == 8 || newLayerId == 16 || newLayerId == 24 {
                return "rest_map"
            } else {
                switch r.Int63() % 6 {
                case 0:
                    if choice == "left" {
                        return "easy_map"
                    } else {
                        return "hard_map"
                    }
                case 1:
                    if choice == "left" {
                        return "hard_map"
                    } else {
                        return "easy_map"
                    }
                case 2:
                    if choice == "left" {
                        return "easy_map"
                    } else {
                        return "boss_map"
                    }
                case 3:
                    if choice == "left" {
                        return "boss_map"
                    } else {
                        return "easy_map"
                    }
                case 4:
                    if choice == "left" {
                        return "hard_map"
                    } else {
                        return "boss_map"
                    }
                case 5:
                    if choice == "left" {
                        return "boss_map"
                    } else {
                        return "hard_map"
                    }
                }
            }
        }
    }
}

当时我手打的，我也看到过这段代码，但当时我看了半天，只做了一件事情，测试了一下选择"left"和选择“right”门，简单、困难和Boss地图的几率是不是一样的，我发现次数足够大时，是一样的，当时也就放弃了，其实本题的奥义就在此。
关键代码是这句：

r := rand.New(rand.NewSource(time.Now().UnixNano()))

首先随机种子在每一次new_level之后只取一次，后面都是用这个随机种子生成的rng去生成随机数，如果我们能知道这个随机数，那岂不是开了天眼，每次都选择easy map即可，那怎么才能知道这个随机数呢？

看一下Go的官方库rng随机数的实现：

// Seed uses the provided seed value to initialize the generator to a deterministic state.
func (rng *rngSource) Seed(seed int64) {
    rng.tap = 0
    rng.feed = rngLen - rngTap

    seed = seed % int32max
    if seed < 0 {
        seed += int32max
    }
    if seed == 0 {
        seed = 89482311
    }

    x := int32(seed)
    for i := -20; i < rngLen; i++ {
        x = seedrand(x)
        if i >= 0 {
            var u int64
            u = int64(x) << 40
            x = seedrand(x)
            u ^= int64(x) << 20
            x = seedrand(x)
            u ^= int64(x)
            u ^= rngCooked[i]
            rng.vec[i] = u
        }
    }
}

敲黑板，注意这句seed = seed % int32max，int64的seed会进行截断，而后台服务器使用的是nanoseconds时间戳，也就是后半段表示nanoseconds的时间戳（如果是前半段时间戳，就结束了），官方给出的意思是可以通过枚举所有1～math.MaxInt32的候选种子，看看他们前几个随机的数字是多少，通过开宝箱、进入下一层，玩家是可以观察到，我开的是哪种类型的宝箱，下一层地图是哪种模式，比如我玩到第10层，观察到的结果是：

next Map_mode easy_map
BoxType add_hp_mp
next Map_mode hard_map
BoxType add_hp_mp
next Map_mode easy_map
BoxType add_skill
next Map_mode easy_map
BoxType del_hp
next Map_mode boss_map
BoxType add_hp_mp
next Map_mode boss_map
BoxType add_skill
next Map_mode hard_map
next Map_mode easy_map
BoxType del_hp
next Map_mode hard_map

地图类型和宝箱类型都能通过代码，推算出随机数取4或者6模是什么数值，我上面的序列对应序列是0111030221231021，这个自己想下，应该比较容易想明白吧。

那枚举所有1～math.MaxInt32，也通过一样的操作，得到可能的宝箱和地图类型序列，结果存在一个map中，key是宝箱和地图类型序列，value就是seed，用自己观察到的序列查询下map，既可以找到这个seed。

我试了下，如果要枚举所有的math.MaxInt32种子，还是很耗时的，当然完全通过并行计算，拆成30个并发任务，每个任务算个1亿多的种子，这也行，但是有参赛的极客想到了一个更好的策略，假设服务器的时间和客户端相差不大，在客户端记录下发送请求的nanosecond时间戳，然后加减10ms，去寻找这个时间戳，我自己试了下，前后10ms没有找到，然后我扩大范围，每扩大10ms，要多计算1000w的种子，我扩大到向后100ms时，激动人心的一刻到来了，我终于找到了：

1655533609434000000...
1655533609435000000...
1655533609436000000...
1655533609437000000...
1655533609438000000...
1655533609439000000...
1655533609440000000...
find key=[1655533609394757619]

其实，尽管在知道了反向查找随机种子之后，我还是花了非常久时间，大概有5～6个小时，才准确找到这个随机种子的，非常不容易，看来任何事情都是知易行难。但是尽管辛苦，我觉得很值得，我要求自己不仅要得到好的结果，也要用正确的方法得到好的结果，这样才是思考解决问题的正确方式吧。

整个极客赛过程，都是自己和自己较劲，我真的想了很多方法，包括一上来通过抓包，慢慢摸索游戏的规律，后来写bfs找每次击败怪兽的最优策略，到后面靠运气通关，然后再去思考怎么样通过破解随机种子开天眼，想想是不是一步步成长的过程，一步步通过对的思维和方法解决问题的过程。

哦，对了，这题充分说明，不要使用时间戳做随机种子，随机种子不要固定下来，嗯，否则是有可能让别人通过观察数据破解的，当然前提是对方猜测到了你的实现方式。

上海疫情封在家中有三个月，辅导了小孩子功课，每每小孩遇到不会做的题目，比她更着急。有时也会想起自己学生时代的样子，遇到难题，心中升起必须克服难题的决心，现在自己娃，怎么没有我当年的风采了。哈哈，扯远了，这两天网上看到一道小学二年级的题目，其实我之前做过类似的题目，但是当下还是震惊了，怎么现在小学二年级题目有这么难？

题目是这样的：

配合网友的回复，我马上想到了之前类似的问题，说是25匹马，5个赛道，至少比几场保证找出最快的2匹马。赛马这题答案我记得很清楚7场比赛，先分组进行小组赛：

首先一个虚线框就是一场比赛，上来25匹马，分5组，进行5场预赛。5组比赛会得到组内的名次，比如A组，A1->A2->A3->A4->A5，每组第一名就是A1，B1，C1，D1和E1，然后第一名之间安排一场决赛：

假设结果就是A1->B1->C1->D1->E1(真正结果不重要，不管怎么样，总能推理出最后的结论)，这时候我们就通过4场比赛，知道了第一名是A1，那第二名是谁呢，是不是B1，不一定哦，有可能是在小组赛中被A1淘汰的A2，所以安排场附加赛吧，A2 vs B1：

附加赛之后，就能知道前两名了。话说回小学二年级赛车这道题目，其实思路一模一样，就是通过小组赛->决赛->附加赛，完成前两名的确认，也就是说赛车的话，通过至少5场比赛，保证找出前两名的赛车。

作为小学二年级的题目很变态了吧，但是出题的人还多问了一句，怎么证明这件事情呢，为什么通过4场比赛一定不能保证找出前两名呢？这个证明难倒我了，抓耳挠腮半天，没想出来。然后我就看了下出题老师的分析，茅塞顿开，原来还可以使用图论+反正法来证明。大致的过程如下：
首先把每一辆赛车想象成点，那么我们一共有9辆赛车，一共9个点，每场比赛，只能进行3辆赛车的比拼，每次比拼完，我们会有一个名次，紧挨着的前后两名之间，使用一条有向边连接，这个我文字讲得有点绕口，一图解千愁：

圆圈表示赛车，1号比2号快，2号比3号快，所以每次比赛，我们仅仅能得到2条有向边，如果进行4场比赛，那么总共的有向边数量是4*2 = 8条，而赛车的数量是9，也就是节点数量是9，8条边，9个点，如果要保证所有边都连接到一张图中，不能出现环，否则边的数量不够。

出现环就意味着9个点形成了若干个分开的子图，上面图中9个节点，分为了两个子图，那么就会有一个问题，第一名都不知道是谁，为什么？因为在1～8节点所在的图中，1号赛车最快，9号赛车单独成子图，9号赛车和谁都没有比过，那么到底9号和1号赛车谁快呢？不知道。所以8条边，安排的比赛结果，划分为多个子图，这样是无法确认前两名的。

那我们4场比赛的结果，如何是可以前两名的图形呢，如下：

左边就是分3场比赛（1、4、7，2、5、8和3、6、9分别比赛），得到结果后，4、2、3比一次，结果是4->2->3，转化这张单图，得到右侧的结果，其实就是一个树形的图，那么前两名就是1、4号赛车。

这样我们很容易举出反例，你不是就8条边么，我最后4、2、3的结果是2->4->3，图就变成非树形图，如下：

这样又回到之前多个子图的问题，我们是没法确认1号赛车和2号赛车谁快的，也就没法真正确认前两名是哪两辆赛车。

OK，至少5场比赛，而非4场比赛保证找出最快的2辆赛车得证。是不是挺难的，至少我是没有想出来，通过图论+反证法证明这个数据结论，由衷发出感慨，活学活用好难啊，能做到的大佬，真的太强了。

导语

Redis Scan 命令在实际生产环境中，业务上的在线场景，应该用的不多，但是在某些离线场景，还是有用武之地的，比如对大key的删除（SET、HASH），可以使用Scan进行迭代处理。

KEYS 与 SCAN

由于 Redis 是单线程在处理用户的命令，而 Keys 命令会一次性遍历所有 Key，于是在 命令执行过程中，无法执行其他命令。这就导致如果 Redis 中的 key 比较多，那么 Keys 命令执行时间就会比较长，从而阻塞 Redis。
所以很多教程都推荐使用 Scan 命令来代替 Keys，因为 Scan 可以限制每次遍历的 key 数量。
Keys 的缺点：
没有limit，我们只能一次性获取所有符合条件的key，如果结果有上百万条，那么等待你的就是“无穷无尽”的字符串输出。
keys命令是遍历算法，时间复杂度是O(N)。如我们刚才所说，这个命令非常容易导致Redis服务卡顿。因此，我们要尽量避免在生产环境使用该命令。
相比于keys命令，Scan命令有两个比较明显的优势：
1）Scan命令的时间复杂度虽然也是O(N)，但它是分次进行的，不会阻塞线程。
2）Scan命令提供了 count 参数，可以控制每次遍历的集合数。
SCAN的命令语法：
SCAN cursor [MATCH pattern] [COUNT count]
cursor - 游标。
pattern - 匹配的模式。
count - 指定每次遍历多少个集合。
可以简单理解为每次遍历多少个元素
根据测试，推荐 Count大小为 1W。

Scan 返回值为数组，会返回一个游标+一系列的 Key。
大致用法如下：
SCAN命令是基于游标的，每次调用后，都会返回一个游标，用于下一次迭代。当游标返回0时，表示迭代结束。
第一次 Scan 时指定游标为 0，表示开启新的一轮迭代，然后 Scan 命令返回一个新的游标，作为第二次 Scan 时的游标值继续迭代，一直到 Scan 返回游标为0，表示本轮迭代结束。
通过这个就可以看出，Scan 完成一次迭代，需要和 Redis 进行多次交互。
按官方命令手册说明，Scan 命令有如下缺陷：

• 同一个元素可能会被返回多次。 处理重复元素的工作交由应用程序负责， 比如说， 可以考虑将迭代返回的元素仅仅用于可以安全地重复执行多次的操作上；
• 如果一个元素是在迭代过程中被添加到数据集的， 又或者是在迭代过程中从数据集中被删除的， 那么这个元素可能会被返回， 也可能不会， 这是未定义的（undefined）；
  另外，注意Scan命令的性能和参数Count有关：

原文链接：https://docs.keydb.dev/blog/2020/08/10/blog-post/
​

Scan背后的原理

先贴下源码：

unsigned long dictScan(dict *d,
                       unsigned long v,
                       dictScanFunction *fn,
                       void *privdata)
{
    dictht *t0, *t1;
    const dictEntry *de;
    unsigned long m0, m1;
​
​
    if (dictSize(d) == 0) return 0;
​
​
    if (!dictIsRehashing(d)) {//没有在做rehash，所以只有第一个表有数据的
        t0 = &(d->ht[0]);
        m0 = t0->sizemask;
        //槽位大小-1,因为大小总是2^N,所以sizemask的二进制总是后面都为1,
        //比如16个slot的字典，sizemask为00001111
​
​
        /* Emit entries at cursor */
        de = t0->table[v & m0];//找到当前这个槽位，然后处理数据
        while (de) {
            fn(privdata, de);//将这个slot的链表数据全部入队，准备返回给客户端。
            de = de->next;
        }
​
​
    } else {
        t0 = &d->ht[0];
        t1 = &d->ht[1];
​
​
        /* Make sure t0 is the smaller and t1 is the bigger table */
        if (t0->size > t1->size) {//将地位设置为
            t0 = &d->ht[1];
            t1 = &d->ht[0];
        }
​
​
        m0 = t0->sizemask;
        m1 = t1->sizemask;
​
​
        /* Emit entries at cursor */
        de = t0->table[v & m0];//处理小一点的表。
        while (de) {
            fn(privdata, de);
            de = de->next;
        }
​
​
        /* Iterate over indices in larger table that are the expansion
            * of the index pointed to by the cursor in the smaller table */
        do {//扫描大点的表里面的槽位，注意这里是个循环，会将小表没有覆盖的slot全部扫描一次的
            /* Emit entries at cursor */
            de = t1->table[v & m1];
            while (de) {
                fn(privdata, de);
                de = de->next;
            }
​
​
            /* Increment bits not covered by the smaller mask */
            //下面的意思是，还需要扩展小点的表，将其后缀固定，然后看高位可以怎么扩充。
            //其实就是想扫描一下小表里面的元素可能会扩充到哪些地方，需要将那些地方处理一遍。
            //后面的(v & m0)是保留v在小表里面的后缀。
            //((v | m0) + 1) & ~m0) 是想给v的扩展部分的二进制位不断地加1，来造成高位不断增加的效果。
            v = (((v | m0) + 1) & ~m0) | (v & m0);
​
​
            /* Continue while bits covered by mask difference is non-zero */
        } while (v & (m0 ^ m1));//终止条件是 v的高位区别位没有1了，其实就是说到头了。
    }
​
​
    /* Set unmasked bits so incrementing the reversed cursor
        * operates on the masked bits of the smaller table */
    v |= ~m0;
    //按位取反，其实相当于v |= m0-1 , ~m0也就是11110000,
    //这里相当于将v的不相干的高位全部置为1，待会再进行翻转二进制位，然后加1，然后再转回来
​
​
    /* Increment the reverse cursor */
    v = rev(v);
    v++;
    v = rev(v);
    //下面将v的每一位倒过来再加1，再倒回去，这是什么意思呢，
    //其实就是要将有效二进制位里面的高位第一个0位设置置为1，因为现在是0嘛
​
    return v;
}

Redis使用了Hash表作为底层实现，原因不外乎高效且实现简单。类似于HashMap那样数组+链表的结构。其中第一维的数组大小为2n(n>=0)。每次扩容数组长度扩大一倍。
Scan命令就是对这个一维数组进行遍历。每次返回的游标值也都是这个数组的索引。Count 参数表示遍历多少个数组的元素，将这些元素下挂接的符合条件的结果都返回。因为每个元素下挂接的链表大小不同，所以每次返回的结果数量也就不同。
关于 Scan 命令的遍历顺序，我们可以用一个小栗子来具体看一下：

127.0.0.1:6379> keys *
1) "key2"
2) "key3"
3) "key1"
4) "key4"
127.0.0.1:6379> scan 0 MATCH * COUNT 1
1) "2"
2) 1) "key2"
127.0.0.1:6379> scan 2 MATCH * COUNT 1
1) "3"
2) 1) "key3"
   2) "key1"
127.0.0.1:6379> scan 3 MATCH * COUNT 1
1) "0"
2) 1) "key4"

​
如上所示，SCAN命令的遍历顺序是：0->2->1->3
这个顺序看起来有些奇怪，我们把它转换成二进制：00->10->01->11
可以看到每次这个序列是高位加1的。
普通二进制的加法，是从右往左相加、进位。而这个序列是从左往右相加、进位的。
相关源码：

v = rev(v);v++;v = rev(v);

Redis Scan 命令最终使用的是 reverse binary iteration 算法，大概可以翻译为 逆二进制迭代，具体算法细节可以看一下这个Github 相关讨论
这个算法简单来说就是：
依次从高位（有效位）开始，不断尝试将当前高位设置为1，然后变动更高位为不同组合，以此来扫描整个字典数组。
其最大的优势在于，从高位扫描的时候，如果槽位是2^N个,扫描的临近的2个元素都是与2^(N-1)相关的就是说同模的，比如槽位8时，0%4 == 4%4， 1%4 == 5%4 ， 因此想到其实hash的时候，跟模是很相关的。
比如当整个字典大小只有4的时候，一个元素计算出的整数为5， 那么计算他的hash值需要模4，也就是hash(n) == 5%4 == 1 , 元素存放在第1个槽位中。当字典扩容的时候，字典大小变为8， 此时计算hash的时候为5%8 == 5 ， 该元素从1号slot迁移到了5号，1和5是对应的，我们称之为同模或者对应。
同模的槽位的元素最容易出现合并或者拆分了。因此在迭代的时候只要及时的扫描这些相关的槽位，这样就不会造成大面积的重复扫描。
使用Scan迭代哈希表时，有以下三种情况：
从迭代开始到结束，哈希表不 Rehash；
从迭代开始到结束，哈希表Rehash，但每次迭代，哈希表要么不开始 Rehash，要么已经结束 Rehash；
从一次迭代开始到结束，哈希表在一次或多次迭代中 Rehash。
即再 Rehash 过程中，执行 Scan 命令，这时数据可能只迁移了一部分。
因此，游标的实现需要兼顾以上三种情况。上述三种情况下游标实现的要求如下：
第一种情况比较简单。假设redis的hash表大小为4，第一个游标为0，读取第一个bucket的数据，然后游标返回2，下次读取bucket 2 ，依次遍历。
第二种情况更复杂。假设redis的hash表大小为4，如果rehash后大小变成8。如果如上返回游标(即返回2)，则显示下图：

假设bucket 0读取后返回到cursor 2，当客户端再次Scan cursor 2时，hash表已经被rehash，大小翻倍到8，redis计算一个key bucket如下：
hash(key)&(size-1)
即如果大小为4，hash(key)&11，如果大小为8，hash(key)&111。所以当size从4扩大到8时，2 号bucket中的原始数据会被分散到2 (010) 和 6 (110) 这两个 bucket中。
从二进制来看，size为4时，在hash(key)之后，取低两位，即hash(key)&11，如果size为8，bucket位置为hash(key) & 111，即取低三个位。
所以依旧不会出现漏掉数据的情况。
第三种情况，如果返回游标2时正在进行rehash，则Hash表1的bucket 2中的一些数据可能已经rehash到了的Hash表2 的bucket[2]或bucket[6]，那么必须完全遍历 哈希表2的 bucket 2 和 6，否则可能会丢失数据。
Redis 全局有两个Hash表，扩容时会渐进式的将表1的数据迁移到表2，查询时程序会先在 ht[0] 里面进行查找， 如果没找到的话， 就会继续到 ht[1] 里面进行查找。
具体游标计算代码如下：
Scan 命令中的游标，其实就是 Redis 内部的 bucket。

v = rev(v);
v++;
v = rev(v);
//下面将v的每一位倒过来再加1，再倒回去，这是什么意思呢，
//其实就是要将有效二进制位里面的高位第一个0位设置置为1，因为现在是0嘛
return v;

代码逻辑非常简单，计算过程如下：

大小为 4 时，游标状态转换为 0-2-1-3。
当大小为 8 时，游标状态转换为 0-4-2-6-1-5-3-7
可以看出，当size由小变大时，所有原来的游标都能在大hashTable中找到对应的位置，并且顺序一致，不会遗漏数据。

缩容处理

之所以会出现重复数据，其实就是为了保证扩缩容后数据不丢。
假设当前 hash 大小为 8：
1）第一次先遍历了 0 号槽，返回游标为 4；
2）准备遍历 4 号槽，然后此时发生了缩容，4 号槽的元素也进到 0 号槽了。
3）但是0 号槽之前已经被遍历过了，此时会丢数据吗？
答案就在源码中：

do {
//扫描大点的表里面的槽位，注意这里是个循环，会将小表没有覆盖的slot全部扫描一次的
    /* Emit entries at cursor */
    de = t1->table[v & m1];
    while (de) {
        fn(privdata, de);
        de = de->next;
    }

    /* Increment bits not covered by the smaller mask */
    //下面的意思是，还需要扩展小点的表，将其后缀固定，然后看高位可以怎么扩充。
    //其实就是想扫描一下小表里面的元素可能会扩充到哪些地方，需要将那些地方处理一遍。
    //后面的(v & m0)是保留v在小表里面的后缀。
    //((v | m0) + 1) & ~m0) 是想给v的扩展部分的二进制位不断的加1，来造成高位不断增加的效果。
    v = (((v | m0) + 1) & ~m0) | (v & m0);

    /* Continue while bits covered by mask difference is non-zero */
} while (v & (m0 ^ m1));//终止条件是v的高位区别位没有1了，其实就是说到头了。

​具体计算方法：​

v = (((v | m0) + 1) & ~m0) | (v & m0);

右边的下半部分是v，左边的上半部分是v。(v&m0) 取出v的低位，例如size=4时v&00000011
左半边(v|m0) + 1 将V 的低位设置为1，然后+1 将进位到v 的高位，再次&m0，V 的高位将被取出。
假设游标返回2并且正在rehashing，大小从4变为8，那么M0 = 00000011 v = 00000010
根据公式计算的下一个光标是 ((00000010 | 00000011) +1) & (11111111100) | (00000010 & 00000011) = (00000100) & (11111111100) | (00000000010) = (000000000110) 正好是 6。

总结

Scan Count 参数限制的是遍历的 bucket 数，而不是限制的返回的元素个数
由于不同 bucket 中的元素个数不同，其中满足条件的个数也不同，所以每次 Scan 返回元素也不一定相同
Count 越大，Scan 总耗时越短，但是单次耗时越大，即阻塞Redis 时间边长
推荐 Count 大小为 1W左右
当 Count = Redis Key 总数时，Scan 和 Keys 效果一致
Scan 采用 逆二进制迭代法来计算游标，主要为了兼容Rehash的情况
Scan 为了兼容缩容后不漏掉数据，会出现重复遍历。
即客户端需要做去重处理
核心就是 逆二进制迭代法，比较复杂，而且算法作者也没有具体证明，为什么这样就能实现，只是测试发现没有问题，各种情况都能兼容。
具体算法细节可以看一下这个Github 相关讨论

导语

最近很久没写文章了，一是工作很忙，二封闭在家，我花了不少时间辅导娃的功课，小学二年级第五单元，有这么一道题目，说9个球里面有1个是次品，比其他球轻，使用天平最少几次可以找出那个次品。这题让我联想到了经典的一个面试问题，12个小球里找次品（不知道次品的轻重），天平最少称几次？

小学题目分析

这道小学题目：9个球里面有1个是次品，比其他球轻，使用天平最少几次可以找出那个次品？应该还是比较容易的，先说答案最少2次可以找出次品小球。首先将9个球平均分为3堆：

第一次称完后，无非三种情况：

• 天平左右平衡，那么次品在剩下的3个小球中；
• 天平的左边轻，那么次品在左边的3个小球中；
• 天平的右边轻，那么次品在右边的3个小球中；
  无论哪一种情况，都把次品小球的范围缩小到了在3个小球中找，那么我们接下来再称一次，选择3个小球中的2个，放在天平的左右两端，如下所示：

这一次的结果和第一次一样去进行分类讨论：

• 天平左右平衡，那么次品就是未放上天平的那个小球；
• 天平左边轻，那么次品在就是放在天平左边的小球；
• 天平右边轻，那么次品在就是放在天平右边的小球；
  OK，至此，小学生阶段的分析就此打住了，把答案写上，还算一个优秀的小学生。我追问了我孩子一句，你知道27个小球要称几次么？我孩子一下愣住了，那么更通用的情况，到底要称几次，才能把次品小球从N个球中找出来呢？比如N=100、1000、100000……

通用情况分析

其实这个通用情况也不难阐述，按上面的例子，其实每次称重，都能将范围缩小为原来的1/3，假设称了k次后，范围缩小到1个球的时候，就找到了次品小球，数学公式为：
N*(1/3)^k <= 1
变换上述公式，N <= 3^k，那么如果称2次，N <= 9, 称3次，N <= 27。
变换上述公式，k >= log3(N)，如果N=100，k >= 4.xxxx，向上取整，k=5，以此类推。
使用天平进行测量，每次在不停的消除不确定性，缩小了次品小球的范围。

面试问题分析

面试问题，12个小球里找次品（不知道次品的轻重），天平最少称几次？这比上面的问题难度大多了，但是也还是可以使用类似的方法去分析，只不过，次品小球的情况变多了，比如上面问题告诉你，次品是比较轻的，那么N个球只有N个情况，要么1号小球轻，要么2号小球轻，以此类推，而现在结果可能有2*N中，要么1号轻，要么1号重，要么2号轻，要么2号重，一次类推，原因是你并不知道次品是轻还是重。
举个例子，N = 6的情况下，可能的结果有12个，分别标识为：1L（1号轻），1H（1号重），2L（2号轻），2H（2号重），3L（3号轻），3H（3号重），4L（4号轻），4H（4号重），5L（5号轻），5H（5号重），6L（6号轻），6H（6号重）。
那么我们还是进行测量，第一次这样分：

分三种情况讨论：

• 天平左右平衡，那么次品在5、6两个小球中，剩下有4种情况5L、5H、6L、6H；
• 天平的左边轻右边重，那么次品在1、2、3、4四个小球中，但是剩下的也只有4种情况，分别是1L、2L、3H、4H；
• 天平的左边重右边轻，那么次品在1、2、3、4四个小球中，但是剩下的也只有4种情况，分别是1H、2H、3L、4L；
  那么很简单，如果再测一次，结果平均看应该是4/3 = 1.333…，平均是大于1的，怎么理解呢，其实就是有可能只有1种，有可能有2种。我们继续分析，假如是第一种情况，次品在5、6两球中，我们可以这样称：

5球放左边，前面第一次称出的任何一颗正常球放右边，那么分三种情况讨论：

• 天平左右平衡，那么次品为6球，剩下有2种情况6L、6H；
• 天平的左边轻右边重，那么次品为5球，5球轻了，5L；
• 天平的左边重右边轻，那么次品为5球，5球重了，5H；
  上述天平左右平衡的情况下，还得再称一次，就能得到6球是轻了还是重了。

那如果第一次称的结果不是平衡的，是第二种情况，怎么办呢，也有办法，按如下方式称重第二次，把可能重的两球分左右两边放在天平上，然后一边再放一个可能轻的球，另外一边放正常的球。

称重结果出来后，分三种情况讨论：

• 天平左右平衡，那么次品为2球，2L；
• 天平的左边轻右边重，那么次品1或者4球，1L或者4H；
• 天平的左边重右边轻，那么次品3球，3H；
  只剩下当中那种情况，需要再称一次，即可找到真正的次品，就不展开论述。

第一次称重后的第三种情况，和第二种情况是对成的，所以经过两次测量，基本上把可能的结果压缩到了2次以下，再测一次，必然可以找到次品小球。

面试问题通用情况分析

根据上面例子分析，如果N个球，测量k次，能找到次品小球，不等式为：
2N * (1/3)^k <= 1
=> N <= (3^k)/2
上面仅仅算出的是上限，我们尽心更细致的分析：
第一次我们将N个球分为相等的2堆a个球，加上剩余的b个球，两堆a个球上天平称，分三种情况讨论：

1. 天平左右平衡，那么次品在那堆b个球中，可能性为2b个（要么轻，要么重），那么必须满足如下不等式：
2. • (1/3)^(k-1) <= 1

=> b <= (3^(k-1))/2
=> b <= (3^(k-1)-1)/2 (因为3的k-1次幂为基数，b又只能为整数，所以3^(k-1)减去1，不等式必须满足)

1. 天平左边重右边轻，次品可能在左边的a球中（可能性是左边a个球重），也可能在右边的a球中（可能性是左边a个球重），所以加起来的可能性是2a，那么必须满足如下不等式：
2. • (1/3)^(k-1) <= 1

=> a <= (3^(k-1))/2
=> a <= (3^(k-1)-1)/2 (理由同上)

1. 天平左边轻右边重，这和第2个情况是对成的，直接得到不等式：
2. <= (3^(k-1)-1)/2

所以，N = 2a+b <= (3^k-3)/2。所以我们得到了如下结果：
如果k=2，N <= 6;如果k=3，N <= 12;如果k=4，N <= 39;……
所以有了公式，回答面试问题就变得很简答了，12个小球要保证能找到次品小球，最少要称3次，但是称重的方案，还是非常复杂的。怎么样，是不是非常有趣呢？

结论

今天想写这篇文章，原因是，往往很多的知识，从我们小学时代就开始有了雏形，慢慢地，随着我们长大，问题会慢慢变复杂，我觉得只有多思考，多动脑，从小打好思维的基础，才能在遇到更复杂问题时，充满信心和耐心，解决更大的挑战吧，一起加油吧。

导语

编程之美 4.1 “金刚坐飞机问题”的问题2，难度比问题1大很多。我看了很多遍原文，没完全搞懂问题2的解法思路，只是大概明白原问题被缩小为一个更小的子问题了，然后利用递推的关系式，求得了最后的解。搜索一下 “金刚坐飞机”，参考了几个很不错的分析，得到了自己比较满意的答案。

审题

首先需要搞清楚题意，尤其在两个根本问题上：

• 飞机上总共有多少座位？N？N+1？还是更多？从问题1的官方解答看，飞机上座位总数为N。
• “...乘客们正准备按机票编号（1,2,3...N）依次排队登机。突然来了一只大猩猩（对，他叫金刚）。他也有飞机票，但是...”，金刚的机票编号是否属于闭区间[1,N]？换句话说，所有乘客（包括金刚）的总数是N还是N+1？既然座位总数为N，金刚也有飞机票，飞机也不可能超载，因此，所有乘客（包括金刚）的总数为N。金刚的机票编号也属于闭区间[1,N]。

然后，看一下编程之美的官方答案：第i个乘客坐在自己位置上的概率为N-i+1/N-i+2，既然飞机座位总数为N，根据官方答案，第1个乘客的概率为N/N+1，这显然不符合直觉，直觉应该是N-1/N。根据全概率公式，第1个乘客坐在自己座位上的概率为P(第1个乘客坐在座位1) = P(金刚坐在座位1)P(第1个乘客坐在座位1|金刚坐在座位1) + P(金刚未在座位1)P(第1个乘客坐在座位1|金刚未在座位1) = (1/N)0+(N-1/N)1 = N-1/N。

如何解释这个问题呢？从问题2的官方解答过程“如果n=1或n>i，那么第i个乘客坐在自己位置上的概率为1....”可以推测，官方认为金刚的机票编号为1。官方答案中的i应该不包括1。

答案

到这里，我重新描述一下问题：飞机上有N个座位，座位编号依次为1,2,..N。恰好有N个乘客排队登机，第1个乘客的座位编号是1，第2个乘客的座位编号是2，...，第N个乘客的座位编号是N。每个乘客都应该坐在编号正确的座位上。但是，第1个乘客是不讲道理的金刚，他第一个进入飞机，随便（随机）挑了一个座位坐下。其他乘客敢怒不敢言，只好依次找座位坐下。如果自己的座位没有被占，则坐自己的作为，否则，也像金刚那样随便挑一个座位。现在，求第i个乘客（第1个乘客还是金刚）坐到自己座位的概率是多少？
我计算得到的答案是：

与官方答案是一致的，下面会给出更加详细的计算过程。

计算过程

下面描述计算过程。
令P(i)表示，第i个乘客坐到座位i的概率。
金刚的座位明明是空的，他还要随便占位；其他乘客只有在自己座位被占的情况下，才随便坐。因此，金刚与其他乘客的行为并不相同，需要分开计算。

【算法与数据结构】金刚坐飞机问题

文章背景

编程之美 4.1 “金刚坐飞机问题”的问题2，难度比问题1大很多。

编程之美的官方解法，包括原理分析、概率公式、推导过程等，感觉阐述不够详细，没有完全读懂。

搜索一下 “金刚坐飞机”，参考了几个很不错的分析，得到一个自己觉得比较完整的答案。

仔细审题

首先，仔细审题，有两个细节需要搞清楚：

飞机上总共有多少座位？N？N+1？还是更多？从问题1的官方解答看，飞机上座位总数为N。
“...乘客们正准备按机票编号（1,2,3...N）依次排队登机。突然来了一只大猩猩（对，他叫金刚）。他也有飞机票，但是...”，金刚的机票编号是否属于闭区间[1,N]？换句话说，所有乘客（包括金刚）的总数是N还是N+1？既然座位总数为N，金刚也有飞机票，飞机也不可能超载，因此，所有乘客（包括金刚）的总数为N。金刚的机票编号也属于闭区间[1,N]。

推敲官方答案

然后，看一下编程之美的官方答案：第i个乘客坐在自己位置上的概率为 。
。
既然飞机座位总数为N，根据官方答案，第1个乘客的概率为。实际上，第1个乘客的概率应该为。计算过程如下：
根据全概率公式，第1个乘客坐在自己座位上的概率：

如何解释这个问题呢？从问题2的官方解答过程“如果n=1或n>i，那么第i个乘客坐在自己位置上的概率为1....”可以推测，官方认为金刚的机票编号为1。官方答案中的i应该不包括1。

重新描述问题

到这里，我重新描述一下问题：
飞机上有N个座位，座位编号依次为1,2,..N。恰好有N个乘客排队登机，第1个乘客的座位编号是1，第2个乘客的座位编号是2，...，第N个乘客的座位编号是N。每个乘客都应该坐在编号正确的座位上。但是，第1个乘客是不讲道理的金刚，他第一个进入飞机，随便（随机）挑了一个座位坐下。其他乘客敢怒不敢言，只好依次找座位坐下。如果自己的座位没有被占，则坐自己的作为，否则，也像金刚那样随便挑一个座位。现在，求第i个乘客（第1个乘客还是金刚）坐到自己座位的概率是多少？
我算出的答案为：

与官方答案是一致的，但是本文会给出更加详细的计算过程。

概率计算过程

下面描述计算过程。
令P(i)表示，第i个乘客坐到座位i的概率。
金刚的座位明明是空的，他还要随便占位；其他乘客只有在自己座位被占的情况下，才随便坐。因此，金刚与其他乘客的行为并不相同，需要分开计算。

先计算金刚的概率，显然，P(1)就是金刚坐在1号座位的概率。金刚是第一个随便挑座位的，因此概率为1/N。

再计算其他乘客的概率，核心的计算公式就是上面提到的全概率公式。第2~N个乘客的概率不容易看出，我们根据全概率公式来计算，条件为金刚坐在编号为j的座位上：

其中：
P(K=j)表示，金刚坐在座位j的概率
P(i|K=j)表示，在金刚坐在座位j上的情况下，第i个乘客坐在座位i的概率

显然，金刚坐在位置j的概率均等，都是P(K=j) = 1/N
条件概率P(i|K=j)的计算不太直观，我们先简单分析一下：

• 如果j=1，也就是说金刚居然坐在了自己的座位上，第i个乘客（其实是所有其他乘客）必然能够坐到自己座位，因此P(K=j) = 1。
• 如果j=i，也就是说金刚居然坐在了第i个乘客的座位上，第i个乘客肯定不能坐到自己座位，因此P(K=j) = 0。
• 如果j>i，也就是说，金刚坐了（第i个乘客）后面的座位，不影响前面乘客找座位，第i个乘客（其实是第2~j-1个乘客）必然能够坐到自己座位，因此P(K=j) = 1。
• 如果1<j<i，也就是说，金刚抢了（第i个乘客）前面的座位，肯定会影响第i个乘客（其实是第j~N个乘客）的座位。
  因此，可以初步计算：

这时，只需要计算最后一个条件概率

可以依次计算P(i|K=i-1)，P(i|K=i-2)，...，P(i|K=2)，发现他们的值都为(N-i+1)/(N-i+2)，神奇吧？
最终结果：

自顶向下计算条件概率，那么，1<j<i时，P(i|K=j)到底是怎么计算的呢？下面详细推导一下j=i-1和j=i-2两种情况的计算过程，其他情况可以顺推。

如果金刚坐在了座位i-1上，第i-1个乘客可以选择座位1、i、i+1~N。每种选择的概率均等，为1/(N-i+2)：

• 如果第i-1个乘客选择座位1，则第i个乘客必然能坐到自己座位，概率为1
• 如果第i-1个乘客选择座位i，则第i个乘客必然不能坐到自己座位，概率为0
• 如果第i-1个乘客选择座位i+1~N，则第i个座位必然能坐到自己座位，概率为1
  根据全概率公式，计算推导过程如下：

如果金刚坐在了座位i-2上，第i-2个乘客可以选择座位1、i-1、i~N。每种选择的概率均等，为1/(N-i+3)：

• 如果第i-2个乘客选择座位1，则第i个乘客必然能坐到自己座位，概率为1
• 如果第i-2个乘客选择座位i-1，则第i-1个乘客的选择将影响第i个乘客的概率。此种情况恰好可以递归到P(i|K=i-1)，只要假设第i-2个乘客就是金刚，它坐在了座位i-1上
• 如果第i-2个乘客选择座位i，则第i个乘客必然不能坐到自己座位，概率为0
• 如果第i-2个乘客选择座位i+1~N，则第i个座位必然能坐到自己座位，概率为1
  根据全概率公式，计算推导过程如下：

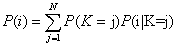
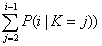
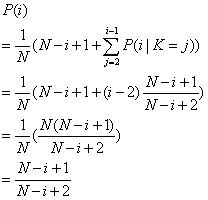
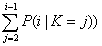如果继续计算下去，其实可以发现规律，P(i|K=j) = (N-i+1)/(N-i+2)，挖掘递归现象，其实，从上述推导的过程中，我们已经发现递归的迹象，是否可以再深入挖掘一下递归公式，进而避免繁琐的推导呢？如果金刚坐在了座位j上，那么第j个乘客将会在座位1、j+1~N中随即选择一个座位。此时，乘客数量变成N-j+1，座位的数量也是N-j+1，第j个乘客恰好是剩余乘客的第1个，他变成了新的金刚。我们把他的座位编号从j换成1，这个变换不会影响问题的答案。下面我们来证明这个变换的安全性。这个变换肯定会影响第j个乘客的概率，但是我们要计算的并不包括第j个乘客，所以不用考虑这个影响。对于第2~i-1个乘客而言，如果第j个乘客无论是坐在1还是j，他们都可以坐在自己的座位上，对他们来说没有区别，对他们的概率也没有任何影响。因此，这个变换是安全的。

从问题的形式上看，变换之后的问题，与原问题等价，只是问题规模从N减小到N-j+1，且每位乘客的编号减小(j-1)，座位编号也减小(j-1)。下面详细描述新问题：
飞机上有N-j+1个座位，座位编号依次为1,2,..N-j+1。恰好有N个乘客排队登机，第1个乘客的座位编号是1，第2个乘客的座位编号是2，...，第N-j+1个乘客的座位编号是N-j+1。每个乘客都应该坐在编号正确的座位上。但是，第1个乘客是不讲道理的金刚，他第一个进入飞机，随便（随机）挑了一个座位坐下。其他乘客敢怒不敢言，只好依次找座位坐下。如果自己的座位没有被占，则坐自己的作为，否则，也像金刚那样随便挑一个座位。现在，求第i个乘客（第1个乘客还是金刚）坐到自己座位的概率是多少？

这里引入了一个新的变量n，表示乘客的总数。我们令F(i,n)表示在乘客总数为n的情况下，第i个乘客坐到自己座位的概率。显然，P(i) = F(i,N)。下面，我们开始计算F(i,n)，首先将P(i,N)计算结果中的N替换成n，然后利用子问题的递归形式。

因此，我们得到了结果：

结合金刚的概率，我们得到完整答案：

参考文章

https://cloud.tencent.com/developer/article/1062061
https://bbs.huaweicloud.com/blogs/312379
https://www.cnblogs.com/python27/archive/2012/04/08/2438009.html